Recall a basic problem that consistent hashing is trying to solve: We have a cache distributed over $N$ machines. Given a string $x \in \Sigma^*$ (e.g., a URL), we want to quickly figure out which of the $N$ machines we should check for the cached data $\mathsf{data}(x)$ (if $x$ is a URL, then $\mathsf{data}(x)$ would be the associated web content).

One solution is to use a standard hash function $H : \Sigma^* \to \{0,1,\ldots,2^{32}-1\}$ (which, say, gives 32-bit outputs), and then agree to store the cached copy of $\mathsf{data}(x)$ on machine \[ H(x) \bmod N \]

The problem with this approach is that $N$ may change over time. This is especially problematic in modern environments in the cloud, when distributed filesystems may be stored across a dynamic environment of virtual machines which are themselves mapped to a dynamic environment of physical machines.

For the standard hashing approach, any change in the value of $N$ will result in most strings $x$ being remapped to different machines, meaning that most of the cache (an approx. $1-1/N$ fraction of entries if we assume our hash function $H$ behaves as a truly random function) will need to be moved or expired.

Hashing servers

Let’s consider a simple approach that addresses this problem: Suppose there are $N$ servers $s_0,s_1,\ldots,s_{N-1}$. We compute the hashes $H(s_0), H(s_1), \ldots, H(s_{N-1})$ of each server, and use the following rule:

For a string $x$: To find the server on which to cache $\mathsf{data}(x)$, we compute $H(x)$ and then go clockwise (modulo $2^{32}$) until we find a location at which some server hashes.

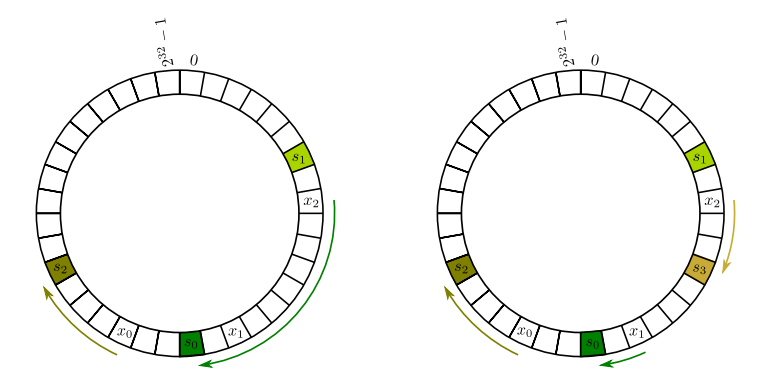
In the first figure, we have servers $s_0,s_1,s_2$. To find the server responsible for caching $\mathsf{data}(x_2)$, we compute $H(x_2)$ and then scan clockwise, eventually finding $s_0$. If a new server $s_3$ is added, then the cache location for $x_0$ and $x_1$ stay the same, while the cache location for $x_2$ changes to $s_3$. (See the second figure.)

If $H$ behaves like a truly random function, then by symmetry the expected load of a server is only $P/N$ when there are $P$ objects cached.

Moreover, the expected number of relocations required for adding an $N$th server is only $P/N$. As opposed to the “standard” approach which relocates a $(1-1/N)$-fraction of pages, consistent hashing only needs to relocate a $1/N$-fraction upon the insertion or deletion of a server.

Implementation

One non-trivial aspect of implementing this data structure is in doing the ``clockwise scan.’’ We want to be able to quickly find the next location modulo $2^{32}$ to which a server hashes.

In other words, we want a data structure that stores keys and, given a value $v$ is able to quickly find the first value $v’ \geq v$ such that $v’$ is one of the keys. (Note that one also have to consider the “wraparound” at $2^{32}$, but this is a simple check.) It turns out that a balanced binary search (like a Red-Black tree) is able to do this in time $O(\log N)$ if the data structure stores $N$ keys.

Note that in some applications, the maximum possible value of $N$ might be fairly small (e.g., 1,000 or 10,000), and then doing an amount of computation proportional to $N$ might be acceptable. For instance, see Rendezvous hashing, which is another simple consistent hashing scheme that works particularly well for small $N$.

Variance reduction

One problem with this approach is that, while the expected load per server is $P/N$ when there are $P$ objects, it can be the case that some servers get significantly overloaded. A nice way to reduce the variance is simply to compute $k$ hashes for each server. So instead of assigning a server $s$ to $H(s)$, we can assign it to locations $H(s \circ 1), \ldots, H(s \circ k)$ for some small number $k$. For instance, in the next figure, we have $k=4$.

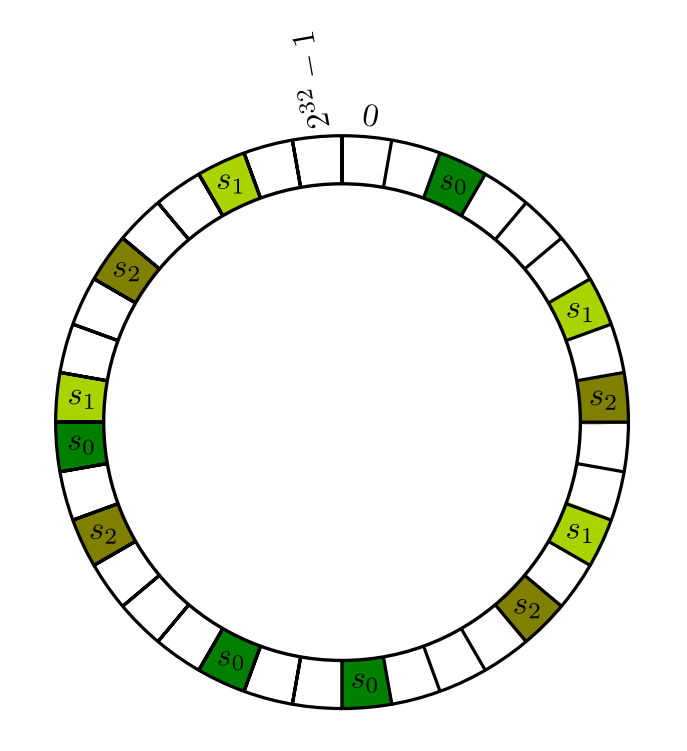
It turns out that taking $k \approx \log_2 N$, we can obtain bounds which assert that with high probability, no server is overloaded. We will revisit such “concentration” bounds later in the course (you already saw the basic idea in CSE 312 under the name Chernoff bounds).

This is also a nice trick for dealing with heterogeneous servers that have different capacities. For instance, if some server $s$ has twice as many resources, we can create twice as many virtual copies.