Formal Definition: a function is concave if

$f((1-\alpha) a+ \alpha b) \geq (1-\alpha ) f(a)+\alpha f(b) \quad \forall a,b, \quad 0 \le \alpha \le 1$

In a picture, the line between two points is a lower bound on the function evaluated at any point in the line. Here we see an example for $f(x) = -x^2$, $a = -1$, $b = 1.5$.

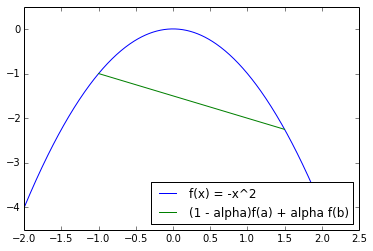
Ok, but is the log likelihood of logistic regression concave?

There are various ways to prove concavity, besides plugging in the definition and working out a lot of math (we just did proof by picture for $f(x) = -x^2$, which is not very formal). One nice way to show concavity (in one dimension) of twice differentiable functions at a certain interval is by looking at the second derivative. If the second derivative is negative on an interval, this means the function 'bends down' (intuitively) on the interval, which only happens if it is concave. In higher dimensions, the equivalent statement is to say that the matrix of second derivatives (Hessian) is negative semi definite. This can be done for the log likelihood of logistic regression, but it is a lot of work (here is an example).

One property of concavity is that the sum of concave functions is a concave functions (can you prove this from the definition?). Therefore, another way to show that a function is concave is by showing that it is the sum of concave functions. If you know some concave functions, it makes proving that other functions are concave a lot easier. In our case, the log likelihood is given by:

$$l(w) =\sum_{j}{y^j(w_0 + \sum_{i=1}^{d}{w_ix_i^j}) - ln(1 + exp(w_0 + \sum_{i=1}^{d}{w_ix_i^j}))}$$

If you happen to know that the first term happens to be a concave function (any function of the form $f(w) = Aw + b$ is called an affine function, and it is concave), and that the second term is a negative log-sum-exp of an affine function (which also happens to be concave), you get that the log likelihood is concave.

A linear classifier is one where a hyperplane is formed by taking a linear combination of the features, such that one 'side' of the hyperplane predicts one class and the other 'side' predicts the other.

Ok, it is concave. Why do we care?

Any local maxima of concave functions are equal to the global maximum. A formal proof is simple, but the intuition is there in the 2-d picture. Note that this is not saying that there is only one vector $w$ that maximizes the log likelihood, but simply that any w that is a local optimum maximizes the log likelihood. The simplest example of a concave function with that has multiple 'optimum solutions' in maximization is the concave function $f(w) = 0$.