Every time we edit and save a document, such as a source code file, this creates a revision. This is automatically true, whether we think about revisions or not.
A version is created consciously by selecting a revision and assigning it a version identifier (e.g., Mozilla 1.4). Sometimes a version is published and becomes a release. Other versions are purely internal.
Say we are maintaining documents on a Unix file system with one file per document.
When we create a new revision, what happens to the old one? It's gone. What if the new revision introduced errors? We'd want to look at the old version to see how the error was introduced. What if we removed a feature that we need to add back?
So we need (1) a way of recording all revisions.
We could try backing up a file before we edit it. We could back up every revision, which would be a lot of work, or back up only important revisions, which requires us to know which revisions are important ahead of time.
Now that we have all these revisions, how do we know which is which? When were they created, which one came from which, what are the differences, etc.? For example, what if all the work for the past week is fatally flawed and we want to back up to the last revision before the week started? What if we want to know the exact revision where a certain bug was introduced?
We need (2) a way of naming revisions and (3) tracking their history.
Large projects have more than one developer. We're going to have problems if two developers try to change a file at the same time. We need (4) a way of managing concurrent development.
Often, revisions form a chain: a file is created as revision 0, edited to form revision 1, which is edited to form revision 2. Other times, we need something more. For example, your company has released Foobar 1.7 from revision 45 of Foobar.java, and is now adding features for the new Foobar 1.8. So far, the developers have created revisions 46, 47, and 48. Then a user reports a bug. You need to be able to fix the bug in revision 45 so you can release a patch, but you're still working on revision 48. So you put the bug fix in revision 45.1, branching the chain. Now you can fix bugs on one branch, and add features on the other. Later, we'll want to merge the bugfixes into the new version, so the branches aren't totally independent. We need a way of (5) branching and merging chains of revisions.
Because of the needs mentioned above, developers do not keep source code files or other important, changing documents as regular system files with arbitrary names. Instead, they use a revision control system with the five properties mentioned above. Note that a revision control system in this sense is a system in the real world, that incorporates developers, users, managers, written policies, computers, etc. However, it turns out to be very difficult to maintain a good revision control system without a lot of software support, so in practice most of it is done by software, which is then called a revision control system. But it still won't do a good job of managing revisions without developers that use it properly.
Software for revision control, such as CVS, helps with all 5 requirements:
CVS is a popular open-source revision control system. See the CVS homepage for downloads and documentation.
Eclipse has built-in CVS support. CVS is accessed through the Team menu which is part of the context menu for Package Explorer items. There are tutorials available on the web.
Part of PA2 is to create a tool for automatically generating lexical analyzers from specifications based on regular expressions. Specifically, you will write code to convert a set of regular expressions with actions to a single NFA with actions.
Recall that a classic NFA has these parts:
The core of the Java representation of an NFA is the NFAState class. Each instance represents one state in an NFA. NFAState has a boolean field to indicate if the state is a final state. The class also has a transition table, giving the next state for each character in the alphabet. The only part of the NFA left is the start state, which is recorded as a separate variable.
But we need a little more information for lexing. (Such as?) We need the action for each final state. Also, to apply the NFA construction rules, it helps to record the start and end state for each NFA.
This is an interpretation process, just like PA1, except that the values are NFAs instead of integers.
If we do that, we end up with "Lexer Tool Alpha", shown below.
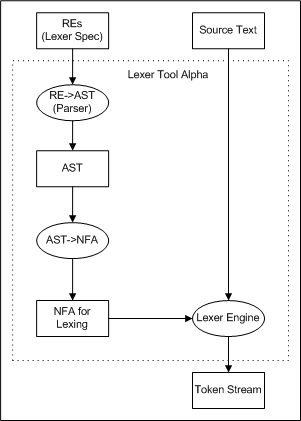
Lexer Tool Alpha includes the "Lexer Engine", which takes an NFA and an input program, and produces the token stream from the program. We'll go over how this works a little later. For now, just assume we've already written it.
All together, Lexer Tool Alpha takes in a spec and an input program, and puts out a token stream. This works fine, but there is an opportunity for improvement. (Which is?) We have to run the RE->AST and AST->NFA processes every time we use the lexer, even though they're always the same.
How do we fix this? Split the tool into a code generator, "Lexer Generator Beta", that runs at lexer-tool build time, and an engine that runs at run-time:
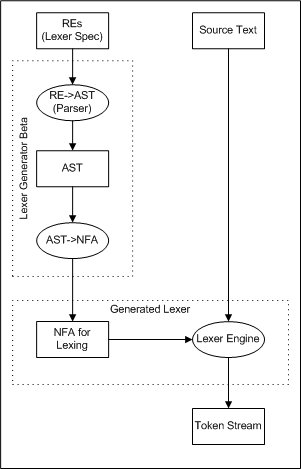
The lexer generator generates the NFA for lexing. Then, we package it together with the lexer engine, and we have a complete lexer that doesn't need to reparse the specification file. The generated lexer is a Java program that takes source text as input and returns a token stream, which is exactly what we want. In a way, Lexer Tool Alpha is an interpreter for lexer specifications, and Lexer Generator Beta is a compiler.
The only question left is how to implement the "NFA for Lexing" box in this diagram. We represent NFAs with Java objects, but the generated lexer consists of code. (So?) A solution is to generate Java code that calls constructors to create the objects. There is still a little to do at runtime, but at least we don't have to do parsing and RE->NFA conversion. We can actually generate the code directly using the traversal, just as before. It's a bit like the pretty-printer, in that we are using a traversal to translate an AST to another form, in this case, Java to create the corresponding NFA.
The lexer engine reads in an NFA, and then runs it on input source text to produce a token stream. This uses the normal algorithm, which you are going to do in the homework. Here are a few of the high points.
At each step, the NFA is in a set of states, so we need a set data structure. We know the universe set ahead of time (all states), so we can use an array of booleans. To run one step, we have an array with the current state set, and an initially empty (all false) array for the next state set. For each state in the current set, find all the states that come next, given the current input, and set them in the next state set. After that, we check for all the epsilon transitions we can take from each state in the next state set, adding any epsilon-reachable states to the set.
The basic idea of lookahead is that when we reach a final state, we don't do the action. Instead we remember the current input position and the action and keep running. Once we get stuck in the NFA, only then do we run the last action that matched, which would be the maximal munch lexeme. We also back up in the input to the remembered position. We know we are stuck when the current state set is the empty set. It is easy to detect this condition using the representation discussed above.
One detail of lookahead is that we need to be able to back up in the input. This requires some kind of buffering. In Java, we can use a PushbackReader, as in the PA2 starter kit.