Beer Mapper

Beer Mapper is a practical implementation of my Active Ranking work on an Apple iPad. The application presents a pair of beers, one pair at a time, from a list of beers that you have indicated you know or have access to and then asks you to select which one you prefer. After you have provided a number of answers, the application shows you a heat map of your preferences over the “beer space.”

How it works - under the hood (scroll down to see app screenshots)
Active ranking requires a low-dimensional embedding of the beers to be applied. Let’s briefly go through how we obtain this embedding.


Two Hearted Ale: 2500+ reviews for just this one beer
We begin with about 10,000 beers from www.ratebeer.com that have at least 50 reviews.
We take all the reviews from each beer and collapse them into a bag of words model. We then weight each word according to the TF*IDF model to get a weighted representation for each beer. Below is an example of this where the size of the word is proportional to its weight.
Once we have a weighted bag of words representation for each beer (a vector of real numbers of dimension about 400,000) we normalize each vector to be norm 1 and find each beer’s 100 nearest neighbors according to Euclidean distance. Below is Two Hearted Ale’s 15 nearest neighbors.
Two Hearted Ale - Weighted Bag of Words:

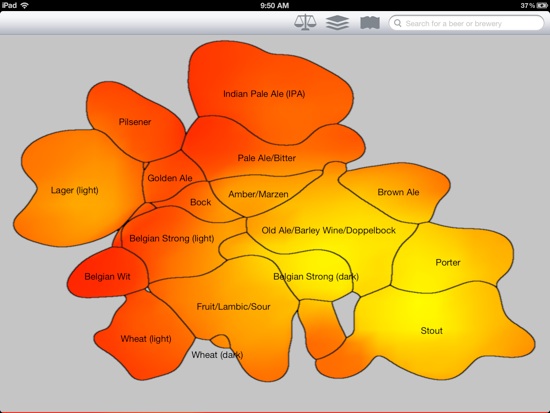
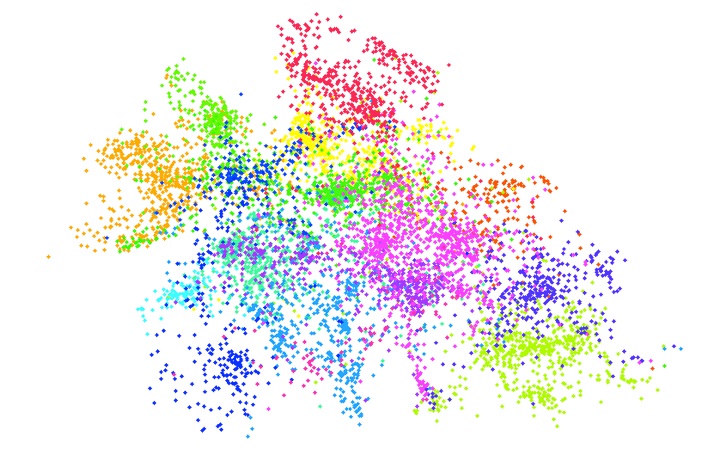
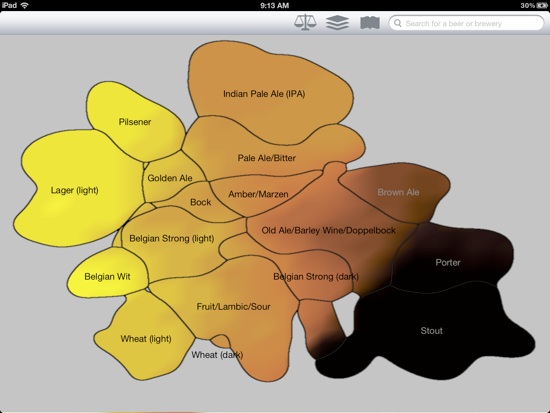
Next we find an embedding of the beers in 2 dimensions that obeys the following property: If A,B,C are three beers and d(A,B) is the distance between beers A and B in the “word space” defined above, then we will solve for an embedding of the beers (X_A, X_B, X_C) such that d(A,B) < d(A,C) iff ||X_A-X_B|| < ||X_A-X_C||. Relations will only be enforced if B or C are a nearest neighbor of A. This is sometimes called non-metric multidimensional scaling (MDS). Because a perfect fit is not possible, we use hinge loss. (One could also implement any number of other non-linear dimensionality reduction techniques like kernel-PCA, local-linear embedding, isomap, etc. but we found this method to produce the most meaningful results.) We get the following embedding, each color representing a different major beer style (style data provided by ratebeer.com was not used in the actual derivation of the embedding) which indicates that the embedding is capturing structure:
Two Hearted Ale - Nearest Neighbors:
Bear Republic Racer 5
Avery IPA
Stone India Pale Ale (IPA)
Founders Centennial IPA
Smuttynose IPA
Anderson Valley Hop Ottin IPA
AleSmith IPA
BridgePort IPA
Boulder Beer Mojo IPA
Goose Island India Pale Ale
Great Divide Titan IPA
New Holland Mad Hatter Ale
Lagunitas India Pale Ale
Heavy Seas Loose Cannon Hop3
Sweetwater IPA
Ratebeer.com also provides measures of color, bitterness, and maltiness for some of the beers. Because we have projected down to a lower dimensional space, we can “complete” missing data where no data about the beer was known.
Color info:
IPA
Pale ale
Brown ale
Porter
Stout
Doppelbock
Belgian dark
Lambic
Wheat
Belgian light
Wit
Light lager
Pilsner
Amber
Blond
“Maltiness” This is a custom, heuristic measure that is a linear combination of the original gravity and final gravity measurements that seem to indicate how malty a beer is, a quantity that has no true definition in reality. Darker is more malty.
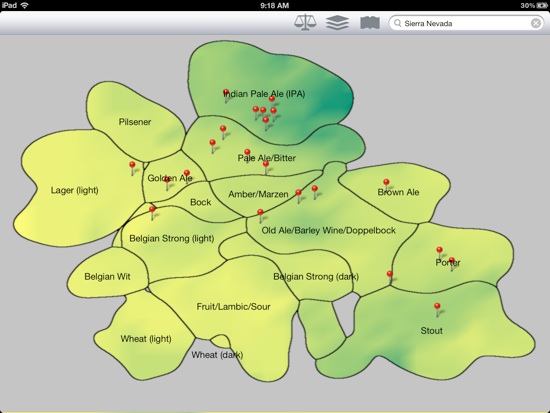
Bitterness info with beers from Sierra Nevada Brewery plotted (darker green means more bitter):
Okay, onto the fun stuff! While in my Active Ranking paper I describe a version of the algorithm that is robust to errors, this algorithm is very fragile with respect to assumptions being violated and tends to ask many more queries than are necessary in practice. Thus, we implemented a Monte-Carlo-like algorithm that is modeled off of Robert Nowak’s Noisy Generalized Binary Search algorithm. Instead of just the two dimensions that are shown to the user, we find a 6 dimensional embedding, apply an RBF kernel to it, and then truncate the kernel matrix to just have 12 dimensions. This 12 dimensional embedding is what is used as the low dimensional embedding in the algorithm. Many heuristics were necessary to get this working fast on an iPad. The result is an algorithm that asks you to compare two beers, one pair at a time. A little bit of information is provided about each beer in case you don’t know the beer too well. Just tap on the beer you prefer:
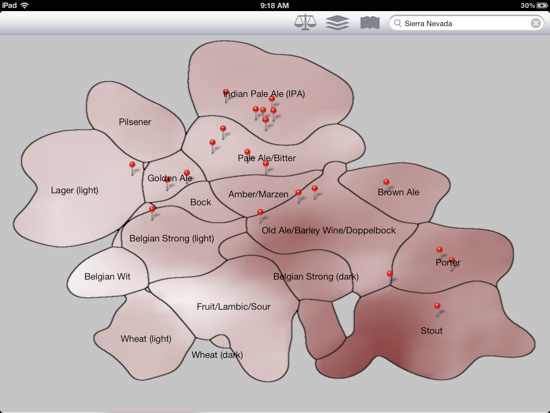
After answering a number of questions we can go back to the “beer space” and plot a heat map of your preferences on just the 2 dimensional embedding (yellow is more preferred which corresponds to the queries I answered):
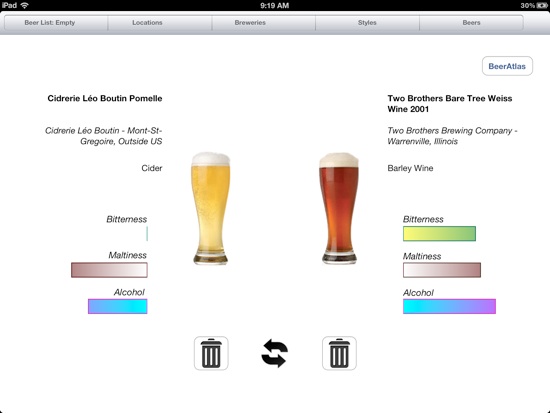
Sorry, no, the app is not on the app store. The app is 97% done but those last few percent are some of the hardest parts like making things a bit more intuitive for the user and providing background code that lets the app run in the background without running down the battery. Maybe some day when I have time...
This website is out of date. I recently teamed up with Savvo to bring the Beer Mapper to market. You can read all about it on the new website. While the basic ideas described here motivated the final version of the app, many of the details have changed.