1988 APCS Free Response

1. Write a function NumDigits that returns the number of digits in the decimal representation of its integer parameter. For example,

   NumDigits(0) = 1, NumDigits(432) = 3, NumDigits(-16) = 2

   YOU WILL RECEIVE NO CREDIT IF YOU USE PASCAL'S PREDEFINED LOGARITHM FUNCTION.

   Write the function body below the following header.

     function NumDigits(Number : integer) : integer;
     { Postcondition: Returns the number of digits in the }
     {                decimal representation of Number.   }
   

2. Elapsed time is conventionally characterized in terms of three quantities: hours, minutes, and seconds. A type, ElapsedTimeType, could be implemented either as a single integer (elapsed seconds) or as three integers (elapsed hours, minutes, seconds) stored as a record with three integer fields.
   1. Suppose that input, output and arithmetic operations for variables of type ElapsedTimeType are to be implemented. Choose one of the two implementations of ElapsedTimeType and list the advantage(s) and disadvantage(s) of that choice.

   2. Write type and variable declarations for the implementation chosen in part (a).

   3. For the implementation chosen in part (a), write a procedure PrintTime that has one parameter of type ElapsedTimeType and that writes the value of its parameter in conventional form

      hh mm ss

      where hh is the number of hours of elapsed time, mm is the number of minutes (in addition to hh hours) of elapsed time, and ss is the number of seconds (in addition to hh hours and mm minutes) of elapsed time.

   4. For the implementation chosen in part (a), write a procedure TimeSum that sets its third parameter to the sum of its first two parameters. All three of the parameters are to be of type ElapsedTimeType.

3. Write a procedure Expand that expands its first argument, M, which is a matrix of numbers, by an amount specified by its second argument, Factor, which is a non-negative integer. (A matrix is a two-dimensional table.) In particular, if M starts with r rows and c columns and if the value of Factor is k, then M is returned as a matrix of k*r rows and k*c columns, where each element e of the original matrix is replaced by a k-by-k matrix, all of whose elements are e.

   The matrix passed to Expand is to be of type MatrixType, which contains a two-dimensional array such that the element in the ith row and jth column of the matrix is in the [i, j] position of the array.

   The effect of the call Expand(M, 3) is shown in the diagram below. (The shaded part represents the unused portion of the array.)

   

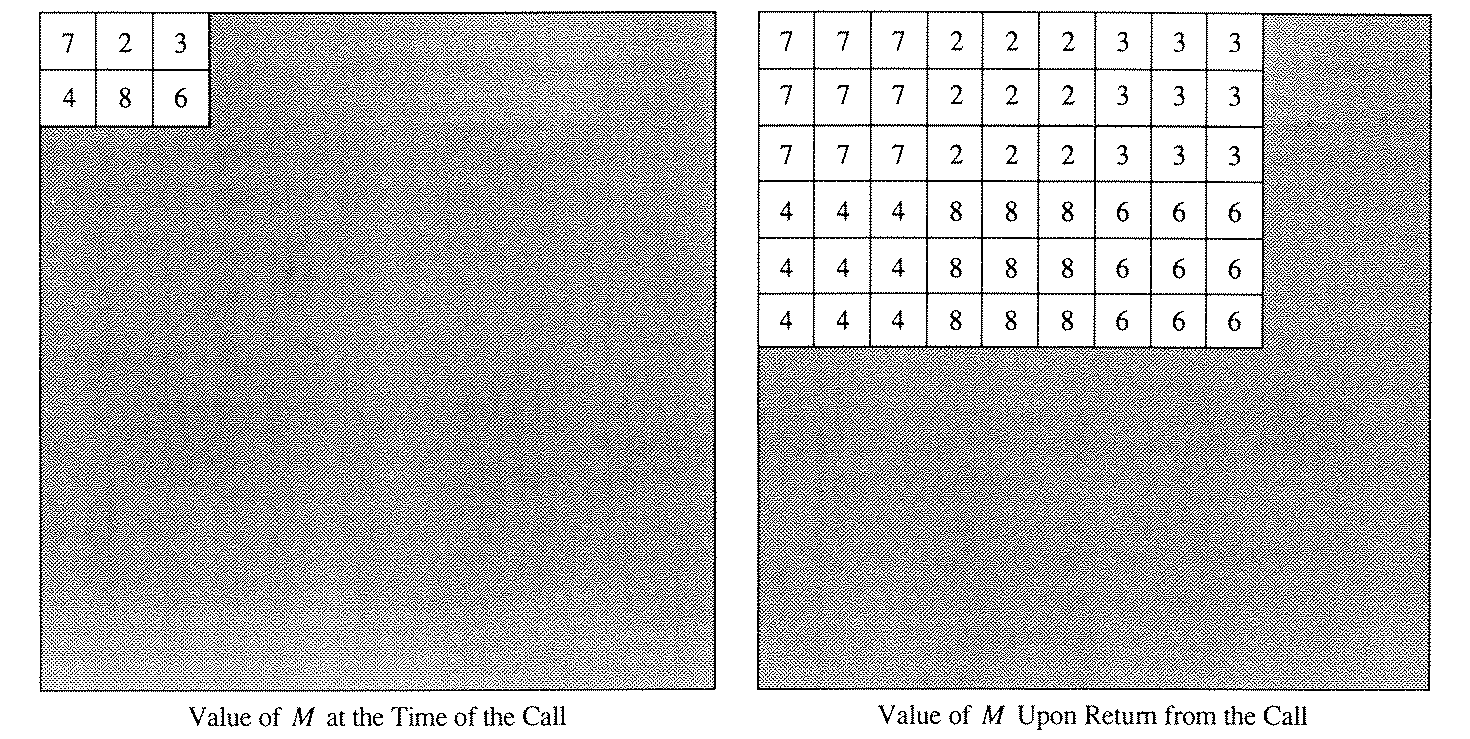
   Assume the following declarations.

     const
       MaxSize = ;
     type
       MatrixArray = array[1..MaxSize, 1..MaxSize] of integer;
       MatrixType = record
                      Numbers : MatrixArray;
                      NumRows : integer;
                      NumCols : integer
                    end;
   

   Because each variable of type MatrixType takes up a significant amount of memory, you cannot assume that a second variable of type MatrixType would fit in memory. Thus, YOU WILL RECEIVE NO CREDIT IF YOU MAKE USE OF ANY ARRAY VARIABLE OTHER THAN THE ONE PASSED INTO THE PROCEDURE.

   You may find it helpful to write and call an auxiliary procedure that assigns a value to every element of a rectangular portion of a two-dimensional array.

   ---

   End of A free response

   ---

4. Write a procedure that reverses the order of the elements of a linked list pointed to by the parameter of the procedure. The list is implemented using the following declarations.

     type
       PtrNode = ^NodeType;
       NodeType = record
                    Data : integer;
                    Next : PtrNode
                  end;
   

   The procedure you are to write is to have the following header.

     procedure Reverse(var Head : PtrNode);
   

5. Trees T1 and T2 are considered to be mirror images of each other.

   

   More formally, the mirror image of a tree T can be specified by a function Mirror, where

   (1) if T has one or zero node(s), then Mirror(T) = T, and

   (2) if T has at least two nodes, as indicated in the figure below.

   

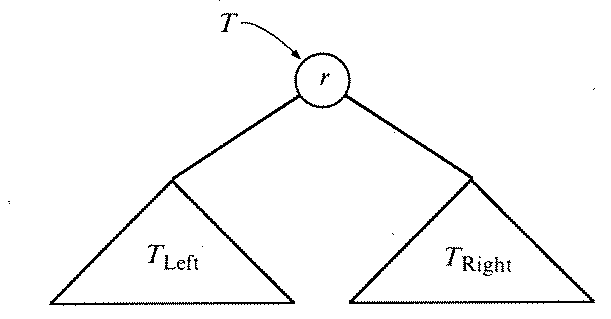
   then Mirror(T) is the tree indicated by

   

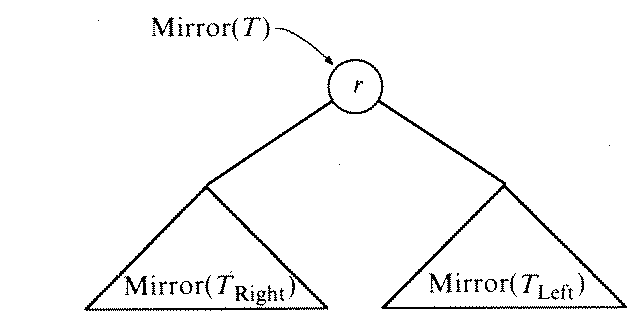
   where r is the value stored at the root of T, while T_Left and T_Right, respectively, are the left and right subtrees of T.Trees are implemented using the following declarations.

     type
       TreeType = ^NodeType;
       NodeType = record
                    Data : DataType;
                    LeftChild,
                    RightChild : TreeType
                  end;
   

   Write a function MirrorTree that constructs the mirror image of the tree passed as the parameter of MirrorTree and that returns a pointer to the constructed tree. The tree passed as the parameter should not be modified by MirrorTree.

Copyright ©1989 by College Entrance Examination Board. All rights reserved.

College Board, Advanced Placement Program, and the acorn logo are registered trademarks of the College Entrance Examination Board.

Permission is hereby granted to any nonprofit organization or institution to reproduce this booklet in limited quantities for its own use, but not for sale, provided that the copyright notices be retained in all reproduced copies exactly as they appear in this booklet. This permission does not apply to any third-party copyrighted material that may be in this booklet.