Block Entropy Analysis of the Indus Script and Natural Languages

 

[September 2010]

 

This page provides additional information for the block entropy plot in Entropy, the Indus script, and language and our IEEE Computer article.

 

 

The figure below (adapted from our IEEE Computer article (Rao, 2010)) plots the block entropies of various types of symbol sequences as the block size is increased from N = 1 to N = 6 symbols. Block entropy generalizes Shannon entropy (Shannon, 1948) as well as the previous measure of bigram conditional entropy in (Rao et al., 2009) to blocks of N symbols. Block entropy for block size N is defined as:

where  are the probabilities of sequences (blocks) of N symbols. Thus, for N = 1, block entropy is simply the standard unigram entropy and for N = 2, it is the entropy of bigrams. Block entropy is useful because it provides a measure of the amount of flexibility allowed by the syntactic rules generating the analyzed sequences (Schmitt & Herzel, 1997): the more restrictive the rules, the smaller the number of syntactically correct combinations of symbols and lower the entropy. Correlations between symbols are reflected in a sub-linear growth of HN with N (e.g., H2 < 2H1).

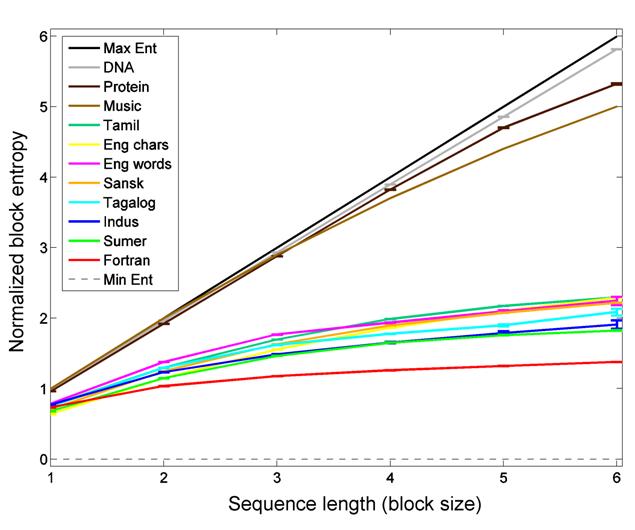
Figure 1: Block entropy scaling of the Indus script compared to natural languages and other sequences. Symbols were signs for the Indus script, bases for DNA, amino acids for proteins, change in pitch for music, characters for English, words for English, Tagalog and Fortran, symbols in abugida (alphasyllabic) scripts for Tamil and Sanskrit, and symbols in the cuneiform script for Sumerian (see (Rao et al., 2009) for details). The values for music are from (Schmitt & Herzel, 1997). To compare sequences over different alphabet sizes L, the logarithm in the entropy calculation was taken to base L (417 for Indus, 4 for DNA, etc.). The resulting normalized block entropy is plotted as a function of block size. Error bars denote 1 standard deviation above/below mean entropy and are negligibly small except for block size 6. (Figure adapted from (Rao, 2010)).

 

The plot shows that the block entropies of the Indus texts remain close to those of a variety of natural languages and far from the entropies for unordered and rigidly ordered sequences (Max Ent and Min Ent respectively). Also shown in the plot for comparison are the entropies for a computer program written in the formal language Fortran, a music sequence (Beethoven Sonata no. 32; data from (Schmitt & Herzel, 1997)), and two sample biological sequences (DNA and proteins). The biological sequences and music have noticeably higher block entropies than the Indus script and natural languages; the Fortran code has lower block entropies (see also Figure 8 in (Schmitt & Herzel, 1997)).

 

These block entropies were estimated using a Bayesian entropy estimation technique known as the NSB estimator (Nemenman et al., 2002), which has been shown to provide good estimates of entropy for undersampled discrete data. We used this technique to counter the relatively small sample size of the Indus corpus (about 1,550 lines of text and 7,000 sign occurrences; see (Yadav et al., 2008) for details regarding the corpus). The Bayesian technique has the added advantage that it also provides an estimate of the standard deviation of the entropy estimate. The standard deviations for the data in the plot above were negligibly small for block sizes less than 6, as can be observed in the figure above.

 

The NSB estimator can be downloaded from here. The NSB parameter values used for the plot above were: qfun=2 (Gauss integration), todo = 1 (nsb integration on), precision=0.1. Details regarding the datasets analyzed can be found in the supplementary information in (Rao et al., 2009). The Tagalog data comprised of text from three books (Ang Bagong Robinson (Tomo 1), Mga Dakilang Pilipino, Ang Mestisa). The values for music in the plot are from (Schmitt & Herzel, 1997).

 

An alternate technique for estimating block entropies is given in (Schmitt & Herzel, 1997). A figure similar to our plot above but with data for DNA, music, English, and Fortran can be found in (Schmitt & Herzel, 1997; Figure 8). Their technique however does not provide an estimate of the standard deviation of the computed entropy value.

 

Similarity in entropy scaling (as in the figure above) by itself is not a sufficient condition to prove that the Indus script (or any other symbol system) is linguistic. However, this similarity increases the posterior probability for the linguistic hypothesis, given other language-like properties of the script (see (Rao et al., 2010) and (Rao, 2010)). Under certain assumptions, one can derive a quantitative estimate of the increase in posterior probability from a result such as Figure 1 above. We refer the reader to (Siddharthan, 2009) for details.

 

 

References

 

Nemenman, Ilya, Fariel Shafee and William Bialek. 2002. Entropy and inference, revisited. Advances in Neural Information Processing Systems 14, MIT Press. http://xxx.lanl.gov/abs/physics/0108025

 

Rao, Rajesh, Nisha Yadav, Mayank Vahia, Hrishikesh Joglekar, R. Adhikari and Iravatham Mahadevan. 2009. Entropic evidence for linguistic structure in the Indus script. Science, 324:1165.

PDF with supplementary information: http://www.cs.washington.edu/homes/rao/ScienceIndus.pdf

 

Rao, Rajesh. 2010. Probabilistic analysis of an ancient undeciphered script. IEEE Computer, 43(4): 76-80.

http://www.cs.washington.edu/homes/rao/ieeeIndus.pdf

 

Rao, Rajesh, Nisha Yadav, Mayank Vahia, Hrishikesh Joglekar, R. Adhikari and Iravatham Mahadevan. 2010. Entropy, the Indus script, and language: A reply to R. Sproat. Computational Linguistics, 36(4).

http://www.cs.washington.edu/homes/rao/IndusCompLing.pdf

 

Schmitt, Armin and Hanspeter Herzel. 1997. Estimating the entropy of DNA sequences. J. Theor. Biol., 1888: 369-377.

 

Shannon, Claude. 1948. A mathematical theory of communication. Bell System Technical Journal, 27:379-423, 623-656.

 

Siddharthan, Rahul. 2009. More Indus thoughts and links.

http://horadecubitus.blogspot.com/2009/05/more-indus-thoughts-and-links.html

 

Yadav N, Vahia MN, Mahadevan I, Joglekar H (2008) A statistical approach for pattern search in Indus writing. International Journal of Dravidian Linguistics 37(1):39-52. http://www.harappa.com/script/tata-writing/indus-script-paper.pdf

 

Back to the Home Page of Rajesh Rao