Publications

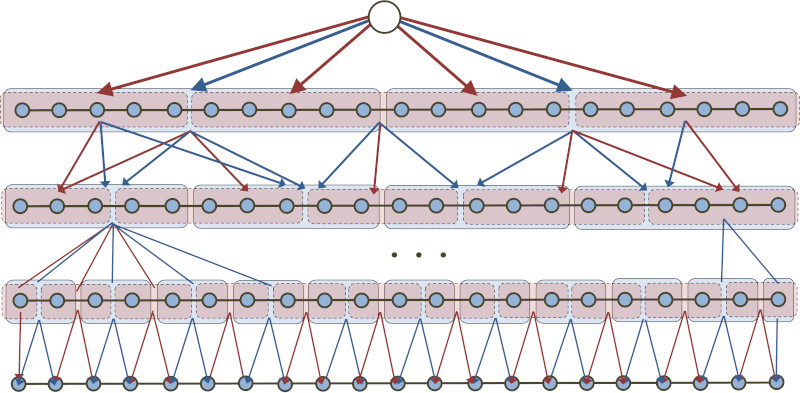
We present an \(O((\log n)^2)\)-competitive algorithm for metrical task systems (MTS) on any \(n\)-point metric space that is also \(1\)-competitive for service costs. This matches the competitive ratio achieved by Bubeck, Cohen, Lee, and Lee (2019) and the refined competitive ratios obtained by Coester and Lee (2019). Those algorithms work by first randomly embedding the metric space into an ultrametric and then solving MTS there. In contrast, our algorithm is cast as regularized gradient descent where the regularizer is a multiscale metric entropy defined directly on the metric space. This answers an open question of Bubeck (Highlights of Algorithms, 2019).

There is a randomized online algorithm for metrical task systems (MTS) that is \(1\)-competitive for service costs and \(O(\log n)\)-competitive for movement costs. In general, these refined guarantees are optimal up to the implicit constant. While an \(O(\log n)\)-competitive algorithm for MTS on HST metrics was developed in BCLL19, that approach could only establish an \(O((\log n)^2)\)-competitive ratio when the service costs are required to be \(O(1)\)-competitive. Our algorithm is an instantiation of online mirror descent with the regularizer derived from a multiscale conditional entropy.

In fact, our algorithm satisfies a set of even more refined guarantees; we are able to exploit this property to combine it with known random embedding theorems and obtain, for any \(n\)-point metric space, a randomized algorithm that is \(1\)-competitive for service costs and \(O((\log n)^2)\)-competitive for movement costs.

We consider metrical task systems on tree metrics, and present an $O(\mathrm{depth} \times \log n)$-competitive randomized algorithm based on the mirror descent framework. For the special case of HSTs, we refine the standard approach based on combining unfair metrical task systems, yielding an $O(\log n)$-competitive algorithm. This is tight up to the implicit constant factor. Using known random embeddings of finite metric spaces into HSTs, this yields an $O((\log n)^2)$-competitive algorithm for general $n$-point spaces.

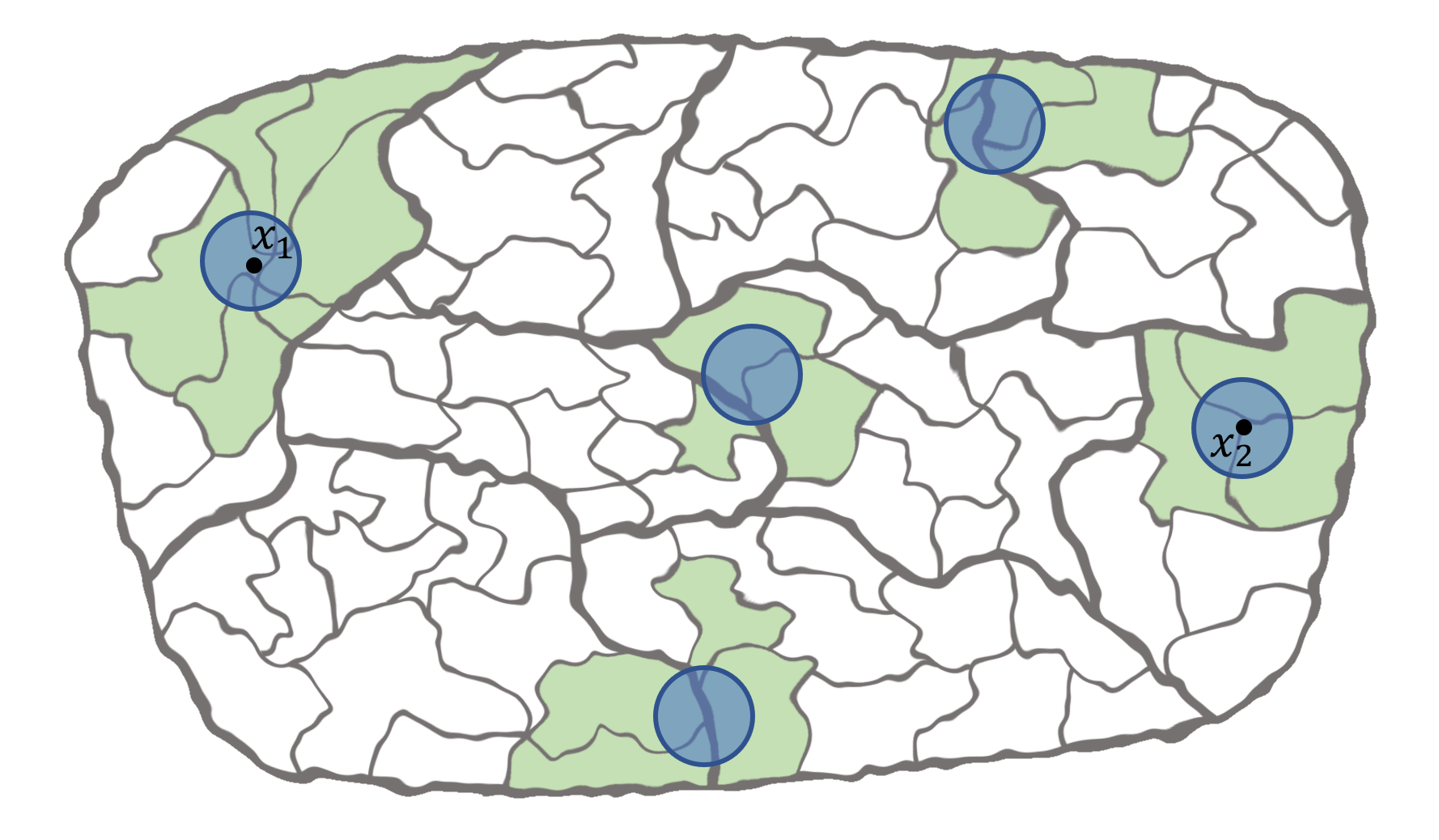
We give a poly(log k)-competitive randomized algorithm for the k-server problem on general metric spaces. The best previous result independent of the underlying metric space is the 2k-1 competitive ratio established for the deterministic work function algorithm by Koutsoupias and Papadimitriou (1995).

Since deterministic algorithms can do no better than k on any metric space with at least k+1 points, this establishes that for every metric space on which the problem is non-trivial, randomized algorithms give an exponential improvement over deterministic algorithms. The approach employs our previous algorithm for the fractional k-server problem on HSTs.

We present an \(O((\log k)^2)\)-competitive randomized algorithm for the k-server problem on hierarchically separated trees (HSTs). This is the first o(k)-competitive randomized algorithm for which the competitive ratio is independent of the size of the underlying HST. Our algorithm is designed in the framework of online mirror descent where the mirror map is a multiscale entropy.

When combined with Bartal’s static HST embedding reduction, this leads to an \(O((\log k)^2 \log n)\)-competitive algorithm on any n-point metric space. We give a new dynamic HST embedding that yields an \(O((\log k)^3 \log \Delta)\)-competitive algorithm on any metric space where the ratio of the largest to smallest non-zero distance is at most \(\Delta\).

We show that if the random walk on a graph has positive coarse Ricci curvature in the sense of Ollivier, then the stationary measure satisfies a \(W^1\) transport-entropy inequality. Peres and Tetali have conjectured a stronger consequence, that a modified log-Sobolev inequality (MLSI) should hold, in analogy with the setting of Markov diffusions. We discuss how our entropy interpolation approach suggests a natural attack on the MLSI conjecture.

Entropy-regularized gradient descent is used to reprove some results from additive combinatorics on the structure of the large Fourier spectrum of dense subsets of the integers.

We introduce a method for proving lower bounds on the efficacy of semidefinite programming (SDP) relaxations for combinatorial problems. In particular, we show that the cut, TSP, and stable set polytopes on n-vertex graphs are not the linear image of the feasible region of any SDP (i.e., any spectrahedron) of dimension less than \(2^{n^c}\), for some constant \(c > 0\). This result yields the first super-polynomial lower bounds on the semidefinite extension complexity of any explicit family of polytopes.

Our results follow from a general technique for proving lower bounds on the positive semidefinite rank of a matrix. To this end, we establish a close connection between arbitrary SDPs and those arising from the sum-of-squares SDP hierarchy. For approximating maximum constraint satisfaction problems, we prove that SDPs of polynomial-size are equivalent in power to those arising from degree-O(1) sum-of-squares relaxations. This result implies, for instance, that no family of polynomial-size SDP relaxations can achieve better than a 7/8-approximation for MAX-3-SAT.

[ PPT slides ]

Best paper award, STOC 2015

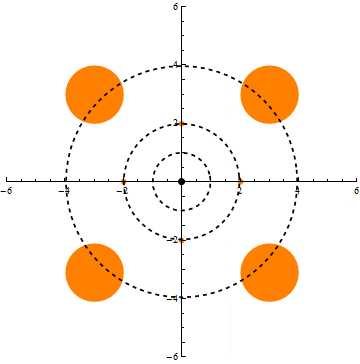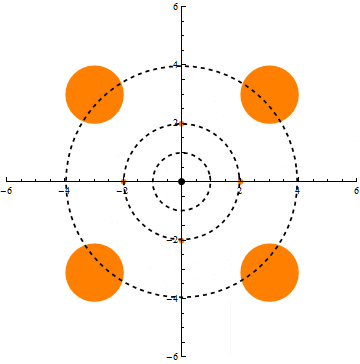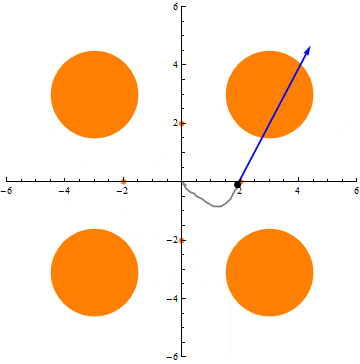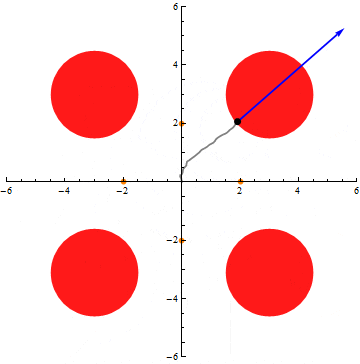
We show that under the Ornstein-Uhlenbeck semigroup (i.e., the natural diffusion process) on n-dimensional Gaussian space, any nonnegative, measurable function exhibits a uniform tail bound better than that implied by Markov’s inequality and conservation of mass. This confirms positively the Gaussian limiting case of Talagrand’s convolution conjecture (1989).

Video: Talagrand’s convolution conjecture and geometry via coupling (IAS)

We prove super-polynomial lower bounds on the size of linear programming relaxations for approximation versions of constraint satisfaction problems. We show that for these problems, polynomial-sized linear programs are exactly as powerful as programs arising from a constant number of rounds of the Sherali-Adams hierarchy. In particular, any polynomial-sized linear program for Max Cut has an integrality gap of 1/2 and any such linear program for Max 3-Sat has an integrality gap of 7/8.

Video: Linear programming and constraint satisfaction (Simons Institute)

Recall the classical hypothesis testing setting with two convex sets of probability distributions $P$ and $Q$. One receives either $n$ i.i.d. samples from a distribution $p \in P$ or from a distribution $q \in Q$ and wants to decide from which set the points were sampled. It is known that the optimal exponential rate at which errors decrease can be achieved by a simple maximum-likelihood ratio test which does not depend on $p$ or $q$, but only on the sets $P$ and $Q$. We consider an adaptive generalization of this model where the choice of $p \in P$ and $q \in Q$ can change in each sample in some way that depends arbitrarily on the previous samples. In other words, in the $k$th round, an adversary, having observed all the previous samples in rounds $1,…,k-1$, chooses $p_k \in P$ and $q_k \in Q$, with the goal of confusing the hypothesis test. We prove that even in this case, the optimal exponential error rate can be achieved by a simple maximum-likelihood test that depends only on $P$ and $Q$.

We then show that the adversarial model has applications in hypothesis testing for quantum states using restricted measurements. For example, it can be used to study the problem of distinguishing entangled states from the set of all separable states using only measurements that can be implemented with local operations and classical communication (LOCC). The basic idea is that in our setup, the deleterious effects of entanglement can be simulated by an adaptive classical adversary. We prove a quantum Stein’s Lemma in this setting: In many circumstances, the optimal hypothesis testing rate is equal to an appropriate notion of quantum relative entropy between two states. In particular, our arguments yield an alternate proof of Li and Winter’s recent strengthening of strong subadditivity for quantum relative entropy.