James R. Lee

We consider the sparsification of sums \(F : \mathbb{R}^n \to \mathbb{R}_+\) where \(F(x) = f_1(\langle a_1,x\rangle) + \cdots + f_m(\langle a_m,x\rangle)\) for vectors $a_1,\ldots,a_m \in \mathbb{R}^n$ and functions $f_1,\ldots,f_m : \mathbb{R} \to \mathbb{R}_+$. We show that $(1+\varepsilon)$-approximate sparsifiers of $F$ with support size $\frac{n}{\varepsilon^2} (\log \frac{n}{\varepsilon})^{O(1)}$ exist whenever the functions $f_1,\ldots,f_m$ are symmetric, monotone, and satisfy natural growth bounds. Additionally, we give efficient algorithms to compute such a sparsifier assuming each $f_i$ can be evaluated efficiently.

Our results generalize the classic case of $\ell_p$ sparsification, where $f_i(z) = |z|^p$, for $p \in (0, 2]$, and give the first near-linear size sparsifiers in the well-studied setting of the Huber loss function and its generalizations, e.g., $f_i(z) = \min{|z|^p, |z|^2}$ for $0 < p \leq 2$. Our sparsification algorithm can be applied to give near-optimal reductions for optimizing a variety of generalized linear models including $\ell_p$ regression for $p \in (1, 2]$ to high accuracy, via solving $(\log n)^{O(1)}$ sparse regression instances with $m \le n(\log n)^{O(1)}$, plus runtime proportional to the number of nonzero entries in the vectors $a_1, \dots, a_m$.

For any norms $N_1,\ldots,N_m$ on $\mathbb{R}^n$ and $N(x) := N_1(x)+\cdots+N_m(x)$, we show there is a sparsified norm $\tilde{N}(x) = w_1 N_1(x) + \cdots + w_m N_m(x)$ such that $|N(x) - \tilde{N}(x)| \leq \epsilon N(x)$ for all $x \in \mathbb{R}^n$, where $w_1,\ldots,w_m$ are non-negative weights, of which only $O(\epsilon^{-2} n \log(n/\epsilon) (\log n)^{2.5} )$ are non-zero.

Additionally, we show that such weights can be found with high probability in time $O(m (\log n)^{O(1)} + \mathrm{poly}(n)) T$, where $T$ is the time required to evaluate a norm $N_i(x)$, assuming that $N(x)$ is $\mathrm{poly}(n)$-equivalent to the Euclidean norm. This immediately yields analogous statements for sparsifying sums of symmetric submodular functions. More generally, we show how to sparsify sums of $p$th powers of norms when the sum is $p$-uniformly smooth.

In a hypergraph on $n$ vertices where $D$ is the maximum size of a hyperedge, there is a weighted hypergraph spectral $\varepsilon$-sparsifier with at most $O(\varepsilon^{-2} \log(D) \cdot n \log n)$ hyperedges. This improves over the bound of Kapralov, Krauthgamer, Tardos and Yoshida (2021) who achieve $O(\varepsilon^{-4} n (\log n)^3)$, as well as the bound $O(\varepsilon^{-2} D^3 n \log n)$ obtained by Bansal, Svensson, and Trevisan (2019).

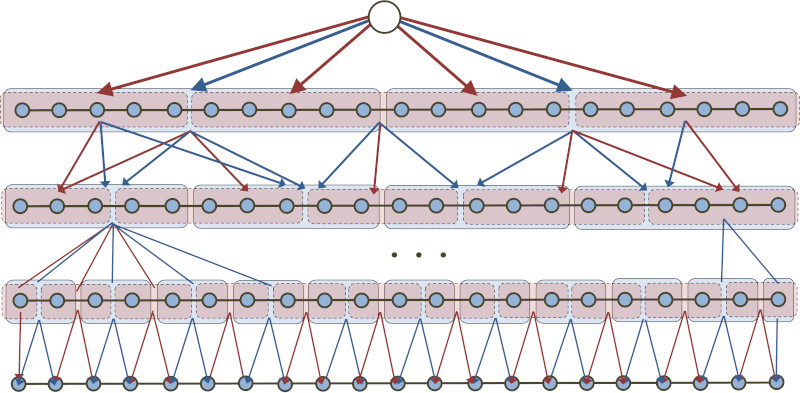
We present an \(O((\log n)^2)\)-competitive algorithm for metrical task systems (MTS) on any \(n\)-point metric space that is also \(1\)-competitive for service costs. This matches the competitive ratio achieved by Bubeck, Cohen, Lee, and Lee (2019) and the refined competitive ratios obtained by Coester and Lee (2019). Those algorithms work by first randomly embedding the metric space into an ultrametric and then solving MTS there. In contrast, our algorithm is cast as regularized gradient descent where the regularizer is a multiscale metric entropy defined directly on the metric space. This answers an open question of Bubeck (Highlights of Algorithms, 2019).

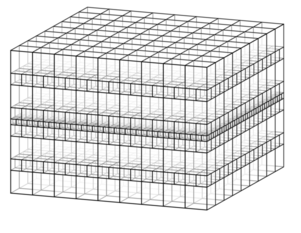
Benjamini and Papasoglou (2011) showed that planar graphs with uniform polynomial volume growth admit $1$-dimensional annular separators: The vertices at graph distance $R$ from any vertex can be separated from those at distance $2R$ by removing at most $O(R)$ vertices. They asked whether geometric $d$-dimensional graphs with uniform polynomial volume growth similarly admit $(d − 1)$-dimensional annular separators when $d > 2$. We show that this fails in a strong sense: For any $d > 3$ and every $s > 1$, there is a collection of interior-disjoint spheres in $\mathbb{R}^d$ whose tangency graph $G$ has uniform polynomial growth, but such that all annular separators in $G$ have cardinality at least $R^s$.

For reversible random networks, we exhibit a relationship between the almost sure spectral dimension and the Euclidean growth exponent, which is the smallest asymptotic rate of volume growth over all embeddings of the network into a Hilbert space. Using metric embedding theory, it is then shown that the Euclidean growth exponent coincides with the metric growth exponent. This simplifies and generalizes a powerful tool for bounding the spectral dimension in random networks.

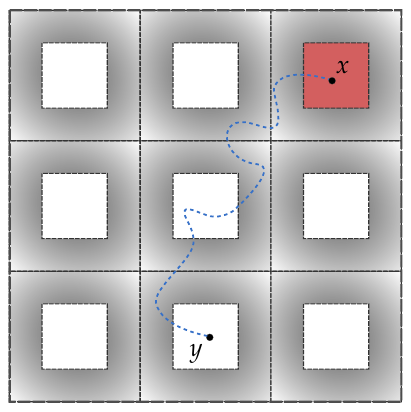
We investigate the validity of the “Einstein relations” in the general setting of unimodular random networks. These are equalities relating scaling exponents:

where $d_w$ is the walk dimension, $d_f$ is the fractal dimension, $d_s$ is the spectral dimension, and $\tilde{\zeta}$ is the resistance exponent. Roughly speaking, this relates the mean displacement and return probability of a random walker to the density and conductivity of the underlying medium. We show that if $d_f$ and $\tilde{\zeta} \geq 0$ exist, then $d_w$ and $d_s$ exist, and the aforementioned equalities hold. Moreover, our primary new estimate $d_w \geq d_f + \tilde{\zeta}$ is established for all $\tilde{\zeta} \in \mathbb{R}$.

This has a number of consequences for unimodular random networks arising from statistical physics.

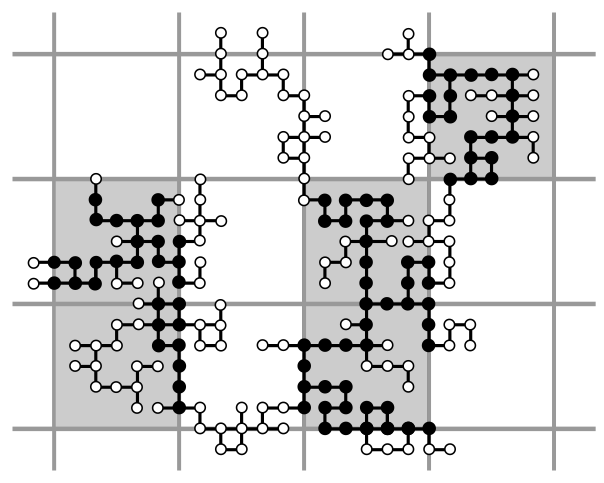
We show that random walk on the incipient infinite cluster (IIC) of two-dimensional critical percolation is subdiffusive in the chemical distance (i.e., in the intrinisc graph metric). Kesten (1986) famously showed that this is true for the Euclidean distance, but it is known that the chemical distance is typically asymptotically larger.

More generally, we show that subdiffusivity in the chemical distance holds for stationary random graphs of polynomial volume growth, as long as there is a multiscale way of covering the graph so that “deep patches” have “thin backbones.” Our estimates are quantitative and give explicit bounds in terms of the one and two-arm exponents.

Consider an infinite planar graph with uniform polynomial growth of degree $d > 2$. Many examples of such graphs exhibit similar geometric and spectral properties, and it has been conjectured that this is necessary. We present a family of counterexamples. In particular, we show that for every rational $d > 2$, there is a planar graph with uniform polynomial growth of degree $d$ on which the random walk is transient, disproving a conjecture of Benjamini (2011).

By a well-known theorem of Benjamini and Schramm, such a graph cannot be a unimodular random graph. We also give examples of unimodular random planar graphs of uniform polynomial growth with unexpected properties. For instance, graphs of (almost sure) uniform polynomial growth of every rational degree $d > 2$ for which the speed exponent of the walk is larger than $1/d$, and in which the complements of all balls are connected. This resolves negatively two questions of Benjamini and Papasoglou (2011).

We present an \(O((\log k)^2)\)-competitive randomized algorithm for the k-server problem on hierarchically separated trees (HSTs). This is the first o(k)-competitive randomized algorithm for which the competitive ratio is independent of the size of the underlying HST. Our algorithm is designed in the framework of online mirror descent where the mirror map is a multiscale entropy.

When combined with Bartal’s static HST embedding reduction, this leads to an \(O((\log k)^2 \log n)\)-competitive algorithm on any n-point metric space. We give a new dynamic HST embedding that yields an \(O((\log k)^3 \log \Delta)\)-competitive algorithm on any metric space where the ratio of the largest to smallest non-zero distance is at most \(\Delta\).

We introduce a method for proving lower bounds on the efficacy of semidefinite programming (SDP) relaxations for combinatorial problems. In particular, we show that the cut, TSP, and stable set polytopes on n-vertex graphs are not the linear image of the feasible region of any SDP (i.e., any spectrahedron) of dimension less than \(2^{n^c}\), for some constant \(c > 0\). This result yields the first super-polynomial lower bounds on the semidefinite extension complexity of any explicit family of polytopes.

Our results follow from a general technique for proving lower bounds on the positive semidefinite rank of a matrix. To this end, we establish a close connection between arbitrary SDPs and those arising from the sum-of-squares SDP hierarchy. For approximating maximum constraint satisfaction problems, we prove that SDPs of polynomial-size are equivalent in power to those arising from degree-O(1) sum-of-squares relaxations. This result implies, for instance, that no family of polynomial-size SDP relaxations can achieve better than a 7/8-approximation for MAX-3-SAT.

[ PPT slides ]

Best paper award, STOC 2015

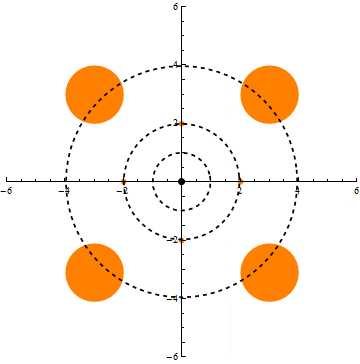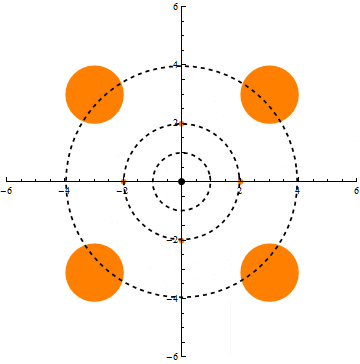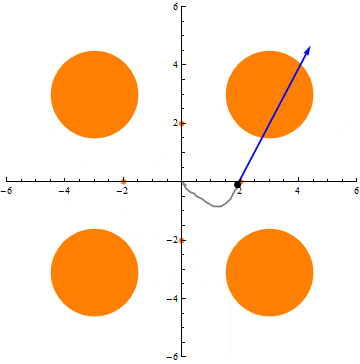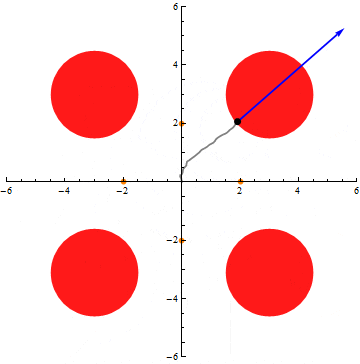
We show that under the Ornstein-Uhlenbeck semigroup (i.e., the natural diffusion process) on n-dimensional Gaussian space, any nonnegative, measurable function exhibits a uniform tail bound better than that implied by Markov’s inequality and conservation of mass. This confirms positively the Gaussian limiting case of Talagrand’s convolution conjecture (1989).

Video: Talagrand’s convolution conjecture and geometry via coupling (IAS)

We prove super-polynomial lower bounds on the size of linear programming relaxations for approximation versions of constraint satisfaction problems. We show that for these problems, polynomial-sized linear programs are exactly as powerful as programs arising from a constant number of rounds of the Sherali-Adams hierarchy. In particular, any polynomial-sized linear program for Max Cut has an integrality gap of 1/2 and any such linear program for Max 3-Sat has an integrality gap of 7/8.

Video: Linear programming and constraint satisfaction (Simons Institute)

A basic fact in spectral graph theory is that the number of connected components in an undirected graph is equal to the multiplicity of the eigenvalue zero in the Laplacian matrix of the graph. In particular, the graph is disconnected if and only if there are at least two eigenvalues equal to zero. Cheeger’s inequality and its variants provide a robust version of the latter fact; they state that a graph has a sparse cut if and only if there are at least two eigenvalues that are close to zero.

It has been conjectured that an analogous characterization holds for higher multiplicities: There are k eigenvalues close to zero if and only if the vertex set can be partitioned into k subsets, each defining a sparse cut. We resolve this conjecture positively. Our result provides a theoretical justification for clustering algorithms that use the bottom k eigenvectors to embed the vertices into \(\mathbb{R}^k\), and then apply geometric considerations to the embedding. We also show that these techniques yield a nearly optimal quantitative connection between the expansion of sets of measure ≈ 1/k and the kth smallest eigenvalue of the normalized Laplacian.

Notes: A no frills proof of the higher-order Cheeger inequality
Related: One hundred hours of lectures from the SGT program at the Simons Institute.
Related: Laurent Miclo uses the higher-order Cheeger inequality for the basis of his resolution of Hoegh-Krohn and Simon’s conjecture that every hyperbounded operator has a spectral gap.

We show that the cover time of a graph can be related to the square of the maximum of the associated Gaussian free field. This yields a positive answer to a question of Aldous and Fill (1994) on deterministic approximations to the cover time, and positively resolves the Blanket Time conjecture of Winkler and Zuckerman (1996).

Video: Cover times of graphs and the Gaussian free field (Newton Institute)
Notes: Majorizing measures and Gaussian processes
Related questions and conjectures (all solved except the one after Lemma 4)

See also the related preprint of Alex Zhai that resolves our main conjecture.

A method is presented for establishing an upper bound on the first non-trivial eigenvalue of the Laplacian of a finite graph. Our approach uses multi-commodity flows to deform the geometry of the graph, and the resulting metric is embedded into Euclidean space to recover a bound on the Rayleigh quotient.

Using this, we resolve positively a question of Spielman and Teng by proving that \(\lambda_2(G) \leq O(d h^6 \log h/n)\) whenever \(G\) is a \(K_h\)-minor-free graph with maximum degree \(d\). While the standard “sweep” algorithm applied to the second eigenvector of a graph my fail to find a good quotient cut in graphs of unbounded degree, the arguments here produce a vector that works for arbitrary graphs. This yields an alterante proof of the Alon-Seymour-Thomas theorem that every excluded-minor family of graphs has \(O(\sqrt{n})\)-node balanced separators.

Related: These methods are extended to higher eigenvalues in a joint work with Kelner, Price, and Teng.
Related: These method form the basis for the uniformization and heat kernel bounds in Conformal growth rates and spectral geometry on distributional limits of graphs.

We prove that the function \(d : \mathbb{R}^3 \times \mathbb{R}^3 \to [0,\infty)\) given by

is a metric on \(\mathbb{R}^3\) such that \((\mathbb{R}^3, \sqrt{d})\) is isometric to a subset of Hilbert space, yet \((\mathbb{R}^3,d)\) does not admit a bi-Lipschitz embedding into \(L_1\). This yields a new simple counter example to the Goemans-Linial conjecture on the integrality gap of the SDP relaxation of the Sparsest Cut problem.

Our methods involve Fourier analytic techniques, combined with a breakthrough of Cheeger and Kleiner, along with classical results of Pansu on the differentiability of Lispchitz functions on the Heisenberg group.

We prove that every \(n\)-point metric space of negative type (and, in particular, every \(n\)-point subset of \(L_1\)) embeds into a Euclidean space with distortion \(O(\sqrt{\log n} \log \log n)\), a result which is tight up to the iterated logarithm factor. As a consequence, we obtain the best known polynomial-time approximation algorithm for the Sparsest Cut problem with general demands. If the demand is supported on a set of size \(k\), we achieve an approximation ratio of \(O(\sqrt{\log k} \log \log k)\).