Publications

We consider the sparsification of sums \(F : \mathbb{R}^n \to \mathbb{R}_+\) where \(F(x) = f_1(\langle a_1,x\rangle) + \cdots + f_m(\langle a_m,x\rangle)\) for vectors $a_1,\ldots,a_m \in \mathbb{R}^n$ and functions $f_1,\ldots,f_m : \mathbb{R} \to \mathbb{R}_+$. We show that $(1+\varepsilon)$-approximate sparsifiers of $F$ with support size $\frac{n}{\varepsilon^2} (\log \frac{n}{\varepsilon})^{O(1)}$ exist whenever the functions $f_1,\ldots,f_m$ are symmetric, monotone, and satisfy natural growth bounds. Additionally, we give efficient algorithms to compute such a sparsifier assuming each $f_i$ can be evaluated efficiently.

Our results generalize the classic case of $\ell_p$ sparsification, where $f_i(z) = |z|^p$, for $p \in (0, 2]$, and give the first near-linear size sparsifiers in the well-studied setting of the Huber loss function and its generalizations, e.g., $f_i(z) = \min{|z|^p, |z|^2}$ for $0 < p \leq 2$. Our sparsification algorithm can be applied to give near-optimal reductions for optimizing a variety of generalized linear models including $\ell_p$ regression for $p \in (1, 2]$ to high accuracy, via solving $(\log n)^{O(1)}$ sparse regression instances with $m \le n(\log n)^{O(1)}$, plus runtime proportional to the number of nonzero entries in the vectors $a_1, \dots, a_m$.

For any norms $N_1,\ldots,N_m$ on $\mathbb{R}^n$ and $N(x) := N_1(x)+\cdots+N_m(x)$, we show there is a sparsified norm $\tilde{N}(x) = w_1 N_1(x) + \cdots + w_m N_m(x)$ such that $|N(x) - \tilde{N}(x)| \leq \epsilon N(x)$ for all $x \in \mathbb{R}^n$, where $w_1,\ldots,w_m$ are non-negative weights, of which only $O(\epsilon^{-2} n \log(n/\epsilon) (\log n)^{2.5} )$ are non-zero.

Additionally, we show that such weights can be found with high probability in time $O(m (\log n)^{O(1)} + \mathrm{poly}(n)) T$, where $T$ is the time required to evaluate a norm $N_i(x)$, assuming that $N(x)$ is $\mathrm{poly}(n)$-equivalent to the Euclidean norm. This immediately yields analogous statements for sparsifying sums of symmetric submodular functions. More generally, we show how to sparsify sums of $p$th powers of norms when the sum is $p$-uniformly smooth.

In a hypergraph on $n$ vertices where $D$ is the maximum size of a hyperedge, there is a weighted hypergraph spectral $\varepsilon$-sparsifier with at most $O(\varepsilon^{-2} \log(D) \cdot n \log n)$ hyperedges. This improves over the bound of Kapralov, Krauthgamer, Tardos and Yoshida (2021) who achieve $O(\varepsilon^{-4} n (\log n)^3)$, as well as the bound $O(\varepsilon^{-2} D^3 n \log n)$ obtained by Bansal, Svensson, and Trevisan (2019).

For reversible random networks, we exhibit a relationship between the almost sure spectral dimension and the Euclidean growth exponent, which is the smallest asymptotic rate of volume growth over all embeddings of the network into a Hilbert space. Using metric embedding theory, it is then shown that the Euclidean growth exponent coincides with the metric growth exponent. This simplifies and generalizes a powerful tool for bounding the spectral dimension in random networks.

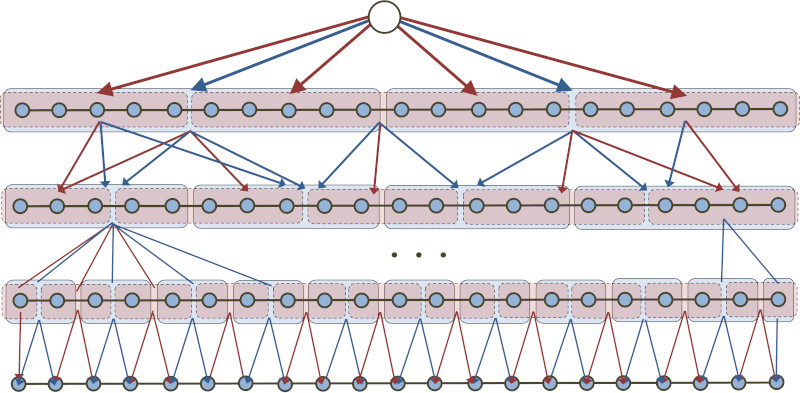
We present an \(O((\log n)^2)\)-competitive algorithm for metrical task systems (MTS) on any \(n\)-point metric space that is also \(1\)-competitive for service costs. This matches the competitive ratio achieved by Bubeck, Cohen, Lee, and Lee (2019) and the refined competitive ratios obtained by Coester and Lee (2019). Those algorithms work by first randomly embedding the metric space into an ultrametric and then solving MTS there. In contrast, our algorithm is cast as regularized gradient descent where the regularizer is a multiscale metric entropy defined directly on the metric space. This answers an open question of Bubeck (Highlights of Algorithms, 2019).

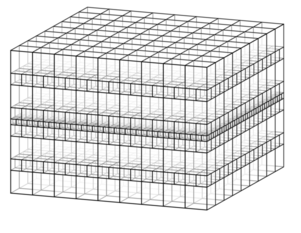
Benjamini and Papasoglou (2011) showed that planar graphs with uniform polynomial volume growth admit $1$-dimensional annular separators: The vertices at graph distance $R$ from any vertex can be separated from those at distance $2R$ by removing at most $O(R)$ vertices. They asked whether geometric $d$-dimensional graphs with uniform polynomial volume growth similarly admit $(d − 1)$-dimensional annular separators when $d > 2$. We show that this fails in a strong sense: For any $d > 3$ and every $s > 1$, there is a collection of interior-disjoint spheres in $\mathbb{R}^d$ whose tangency graph $G$ has uniform polynomial growth, but such that all annular separators in $G$ have cardinality at least $R^s$.

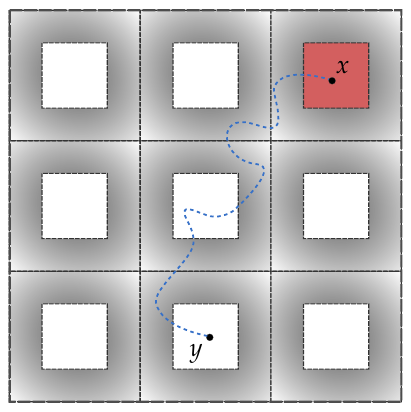
We investigate the validity of the “Einstein relations” in the general setting of unimodular random networks. These are equalities relating scaling exponents:

where $d_w$ is the walk dimension, $d_f$ is the fractal dimension, $d_s$ is the spectral dimension, and $\tilde{\zeta}$ is the resistance exponent. Roughly speaking, this relates the mean displacement and return probability of a random walker to the density and conductivity of the underlying medium. We show that if $d_f$ and $\tilde{\zeta} \geq 0$ exist, then $d_w$ and $d_s$ exist, and the aforementioned equalities hold. Moreover, our primary new estimate $d_w \geq d_f + \tilde{\zeta}$ is established for all $\tilde{\zeta} \in \mathbb{R}$.

This has a number of consequences for unimodular random networks arising from statistical physics.

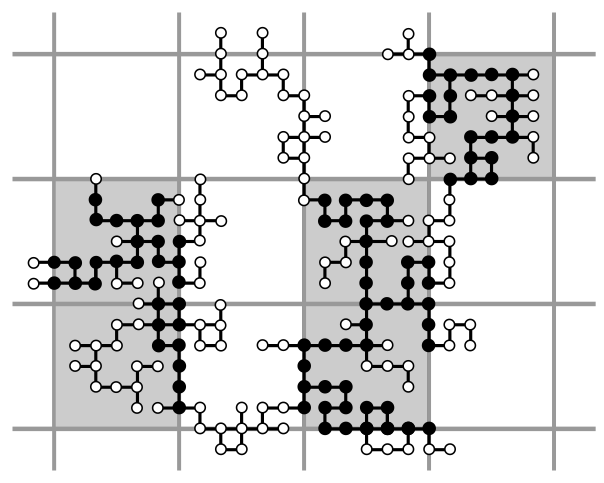
We show that random walk on the incipient infinite cluster (IIC) of two-dimensional critical percolation is subdiffusive in the chemical distance (i.e., in the intrinisc graph metric). Kesten (1986) famously showed that this is true for the Euclidean distance, but it is known that the chemical distance is typically asymptotically larger.

More generally, we show that subdiffusivity in the chemical distance holds for stationary random graphs of polynomial volume growth, as long as there is a multiscale way of covering the graph so that “deep patches” have “thin backbones.” Our estimates are quantitative and give explicit bounds in terms of the one and two-arm exponents.

Consider an infinite planar graph with uniform polynomial growth of degree $d > 2$. Many examples of such graphs exhibit similar geometric and spectral properties, and it has been conjectured that this is necessary. We present a family of counterexamples. In particular, we show that for every rational $d > 2$, there is a planar graph with uniform polynomial growth of degree $d$ on which the random walk is transient, disproving a conjecture of Benjamini (2011).

By a well-known theorem of Benjamini and Schramm, such a graph cannot be a unimodular random graph. We also give examples of unimodular random planar graphs of uniform polynomial growth with unexpected properties. For instance, graphs of (almost sure) uniform polynomial growth of every rational degree $d > 2$ for which the speed exponent of the walk is larger than $1/d$, and in which the complements of all balls are connected. This resolves negatively two questions of Benjamini and Papasoglou (2011).

There is a randomized online algorithm for metrical task systems (MTS) that is \(1\)-competitive for service costs and \(O(\log n)\)-competitive for movement costs. In general, these refined guarantees are optimal up to the implicit constant. While an \(O(\log n)\)-competitive algorithm for MTS on HST metrics was developed in BCLL19, that approach could only establish an \(O((\log n)^2)\)-competitive ratio when the service costs are required to be \(O(1)\)-competitive. Our algorithm is an instantiation of online mirror descent with the regularizer derived from a multiscale conditional entropy.

In fact, our algorithm satisfies a set of even more refined guarantees; we are able to exploit this property to combine it with known random embedding theorems and obtain, for any \(n\)-point metric space, a randomized algorithm that is \(1\)-competitive for service costs and \(O((\log n)^2)\)-competitive for movement costs.

We consider metrical task systems on tree metrics, and present an $O(\mathrm{depth} \times \log n)$-competitive randomized algorithm based on the mirror descent framework. For the special case of HSTs, we refine the standard approach based on combining unfair metrical task systems, yielding an $O(\log n)$-competitive algorithm. This is tight up to the implicit constant factor. Using known random embeddings of finite metric spaces into HSTs, this yields an $O((\log n)^2)$-competitive algorithm for general $n$-point spaces.

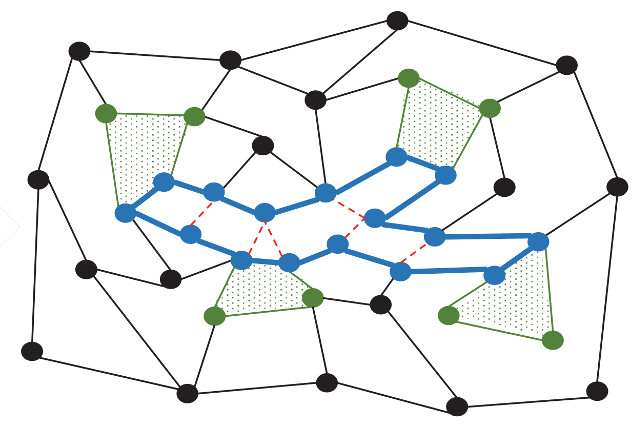
We establish new and improved bounds on the flow-cut gap in planar flow networks where the terminals lie on a small number of faces. The classical Okamura-Seymour theorem (1981) shows that when all terminals lie on a single face, the flow-cut gap is exactly 1. We show that if the terminals lie on $\gamma$ faces, the flow-cut gap is $O(\log \gamma)$. This is proved by embedding the terminal metric into a distribution over trees with distortion $O(\log \gamma)$, which is tight up to the implied constant factor.

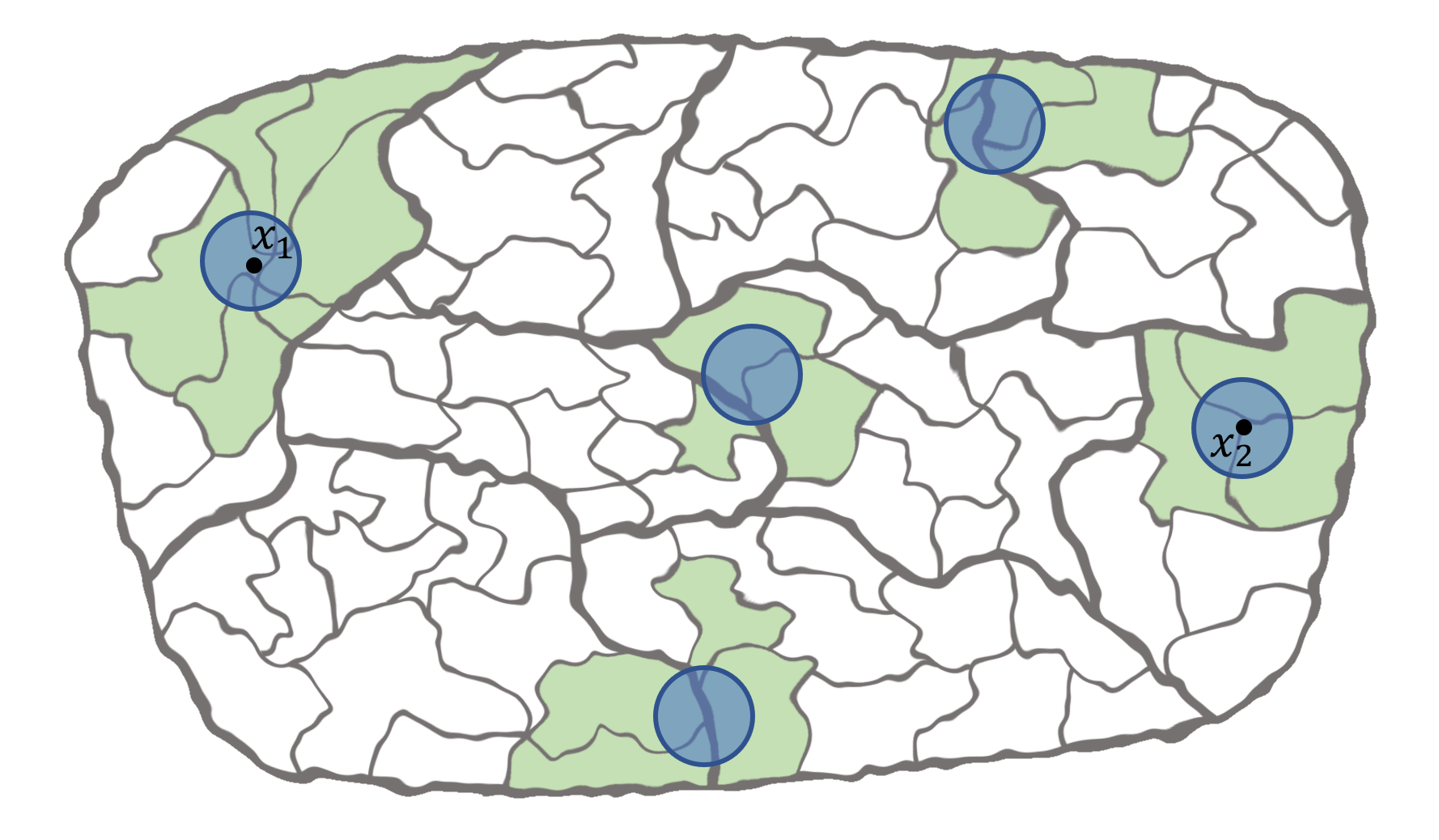
We give a poly(log k)-competitive randomized algorithm for the k-server problem on general metric spaces. The best previous result independent of the underlying metric space is the 2k-1 competitive ratio established for the deterministic work function algorithm by Koutsoupias and Papadimitriou (1995).

Since deterministic algorithms can do no better than k on any metric space with at least k+1 points, this establishes that for every metric space on which the problem is non-trivial, randomized algorithms give an exponential improvement over deterministic algorithms. The approach employs our previous algorithm for the fractional k-server problem on HSTs.

We present an \(O((\log k)^2)\)-competitive randomized algorithm for the k-server problem on hierarchically separated trees (HSTs). This is the first o(k)-competitive randomized algorithm for which the competitive ratio is independent of the size of the underlying HST. Our algorithm is designed in the framework of online mirror descent where the mirror map is a multiscale entropy.

When combined with Bartal’s static HST embedding reduction, this leads to an \(O((\log k)^2 \log n)\)-competitive algorithm on any n-point metric space. We give a new dynamic HST embedding that yields an \(O((\log k)^3 \log \Delta)\)-competitive algorithm on any metric space where the ratio of the largest to smallest non-zero distance is at most \(\Delta\).

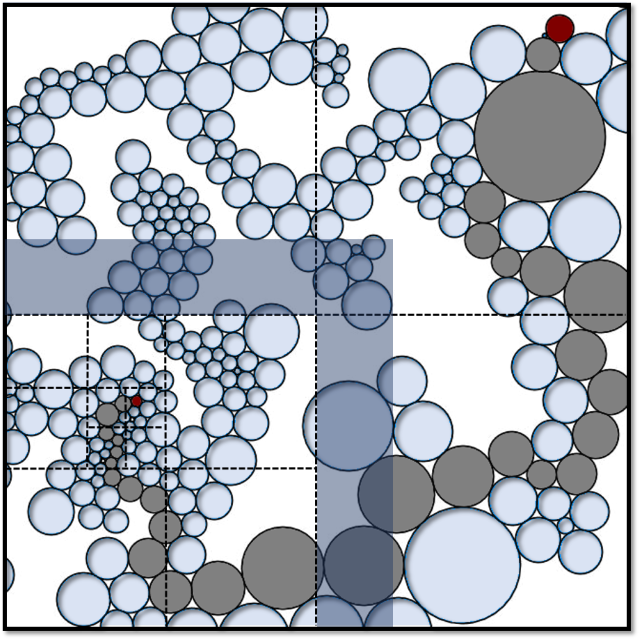
If \((G, \rho)\) is the distributional limit of finite graphs that can be sphere-packed in \(\mathbb{R}^d\), then the conformal growth exponent of \((G, \rho)\) is at most d. In other words, there exists a unimodular “unit volume” weighting of the graph metric on G such that the volume growth of balls is asymptotically polynomial with exponent d. This generalizes to graphs that can be quasisymmetrically packed in an Ahlfors d-regular metric measure space. Using our previous work, it gives bounds on the almost sure spectral dimension of G.

For a unimodular random graph \((G, \rho)\), we consider deformations of its intrinsic path metric by a (random) weighting of its vertices. This leads to the notion of the conformal growth exponent of \((G, \rho)\), which is the best asymptotic degree of volume growth of balls that can be achieved by such a weighting. Under moment conditions on the degree of the root, we show that the conformal growth exponent of a unimodular random graph bounds its almost sure spectral dimension.

For two-dimensional growth, one obtains more precise information about recurrence, the heat kernel, and subdiffusivity of the random walk. In particular, this gives a new method for studying the uniform infinite planar triangulation (UIPT) and quadrangulation (UIPQ).

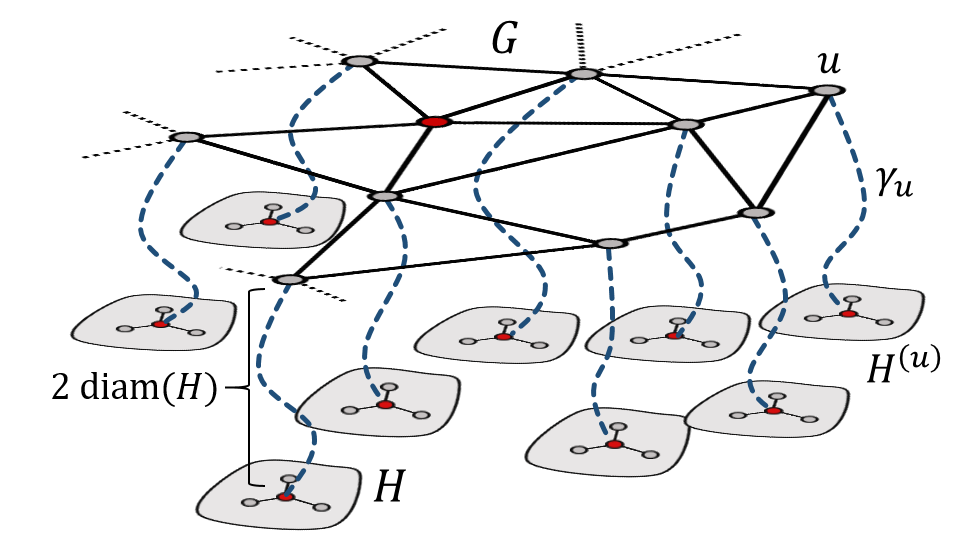
We show that if $(G,\rho)$ is a stationary random graph of annealed polynomial growth, then almost surely there is an infinite sequence of times at which the random walk started from x is at most diffusive. This result is new even in the case when G is a stationary random subgraph of $\mathbb{Z}^d$. Combined with the work of Benjamini, Duminil-Copin, Kozma, and Yadin, it implies that G almost surely does not admit a non-constant harmonic function of sublinear growth.

To complement this, we argue that passing to a subsequence of times is necessary, as there are stationary random graphs of (almost sure) polynomial growth where the random walk is almost surely superdiffisuve at an infinite subset of times.

Addendum: In the paper, we ask whether passing to a subsequence of times is necessary when $G$ is a stationary random subgraph of $\mathbb{Z}^d$. For the case $d=2$, it holds for all times using my paper with Ding and Peres. For $d$ sufficiently large, passing to a subsequence of times is necessary; this can be proved by showing that our stationary random graph occurs as a stationary random subgraph of $\mathbb{Z}^d_{\infty}$, using my paper with Krauthgamer.

A region intersection graph over a base graph \(G_0\) is a graph \(G\) whose vertices correspond to connected subsets of \(G_0\) with an edge between two vertices if the corresponding regions intersect. We show that if \(G_0\) excludes the complete graph \(K_h\) as a minor, then every region intersection graph over \(G_0\) with m edges has a balanced separator with \(O(\sqrt{m})\) nodes. If \(G\) has uniformly bounded vertex degrees, we show the separator is found by spectral partitioning.

A string graph is the intersection graph of continuous arcs in the plane. The preceding result implies that every string graph with m edges has a balanced separator of size \(O(\sqrt{m})\). This bound is optimal, as it generalizes the planar separator theorem. It confirms a conjecture of Fox and Pach (2010) and improves over the \(O(\sqrt{m} \log m)\) bound of Matousek (2013).

We show that if the random walk on a graph has positive coarse Ricci curvature in the sense of Ollivier, then the stationary measure satisfies a \(W^1\) transport-entropy inequality. Peres and Tetali have conjectured a stronger consequence, that a modified log-Sobolev inequality (MLSI) should hold, in analogy with the setting of Markov diffusions. We discuss how our entropy interpolation approach suggests a natural attack on the MLSI conjecture.

Entropy-regularized gradient descent is used to reprove some results from additive combinatorics on the structure of the large Fourier spectrum of dense subsets of the integers.

We introduce a method for proving lower bounds on the efficacy of semidefinite programming (SDP) relaxations for combinatorial problems. In particular, we show that the cut, TSP, and stable set polytopes on n-vertex graphs are not the linear image of the feasible region of any SDP (i.e., any spectrahedron) of dimension less than \(2^{n^c}\), for some constant \(c > 0\). This result yields the first super-polynomial lower bounds on the semidefinite extension complexity of any explicit family of polytopes.

Our results follow from a general technique for proving lower bounds on the positive semidefinite rank of a matrix. To this end, we establish a close connection between arbitrary SDPs and those arising from the sum-of-squares SDP hierarchy. For approximating maximum constraint satisfaction problems, we prove that SDPs of polynomial-size are equivalent in power to those arising from degree-O(1) sum-of-squares relaxations. This result implies, for instance, that no family of polynomial-size SDP relaxations can achieve better than a 7/8-approximation for MAX-3-SAT.

[ PPT slides ]

Best paper award, STOC 2015

We show that under the Ornstein-Uhlenbeck semigroup (i.e., the natural diffusion process) on n-dimensional Gaussian space, any nonnegative, measurable function exhibits a uniform tail bound better than that implied by Markov’s inequality and conservation of mass. This confirms positively the Gaussian limiting case of Talagrand’s convolution conjecture (1989).

Video: Talagrand’s convolution conjecture and geometry via coupling (IAS)

We study the computational power of general symmetric relaxations for combinatorial optimization problems, both in the linear programming (LP) and semidefinite programming (SDP) case. We show new connections to explicit LP and SDP relaxations, like those obtained from standard hierarchies.

We prove super-polynomial lower bounds on the size of linear programming relaxations for approximation versions of constraint satisfaction problems. We show that for these problems, polynomial-sized linear programs are exactly as powerful as programs arising from a constant number of rounds of the Sherali-Adams hierarchy. In particular, any polynomial-sized linear program for Max Cut has an integrality gap of 1/2 and any such linear program for Max 3-Sat has an integrality gap of 7/8.

Video: Linear programming and constraint satisfaction (Simons Institute)

Recall the classical hypothesis testing setting with two convex sets of probability distributions $P$ and $Q$. One receives either $n$ i.i.d. samples from a distribution $p \in P$ or from a distribution $q \in Q$ and wants to decide from which set the points were sampled. It is known that the optimal exponential rate at which errors decrease can be achieved by a simple maximum-likelihood ratio test which does not depend on $p$ or $q$, but only on the sets $P$ and $Q$. We consider an adaptive generalization of this model where the choice of $p \in P$ and $q \in Q$ can change in each sample in some way that depends arbitrarily on the previous samples. In other words, in the $k$th round, an adversary, having observed all the previous samples in rounds $1,…,k-1$, chooses $p_k \in P$ and $q_k \in Q$, with the goal of confusing the hypothesis test. We prove that even in this case, the optimal exponential error rate can be achieved by a simple maximum-likelihood test that depends only on $P$ and $Q$.

We then show that the adversarial model has applications in hypothesis testing for quantum states using restricted measurements. For example, it can be used to study the problem of distinguishing entangled states from the set of all separable states using only measurements that can be implemented with local operations and classical communication (LOCC). The basic idea is that in our setup, the deleterious effects of entanglement can be simulated by an adaptive classical adversary. We prove a quantum Stein’s Lemma in this setting: In many circumstances, the optimal hypothesis testing rate is equal to an appropriate notion of quantum relative entropy between two states. In particular, our arguments yield an alternate proof of Li and Winter’s recent strengthening of strong subadditivity for quantum relative entropy.

There is a constant c > 0 such that for every $\varepsilon \in (0,1)$ and $n \geq 1/\varepsilon^2$, the following holds. Any mapping from the $n$-point star metric into $\ell_1^d$ with bi-Lipschitz distortion $1+\varepsilon$ requires dimension \[d \geq \frac{c \log n}{\varepsilon^2 \log (1/\varepsilon)}.\]

The classical Okamura-Seymour theorem states that for an edge-capacitated, multi-commodity flow instance in which all terminals lie on a single face of a planar graph, there exists a feasible concurrent flow if and only if the cut conditions are satisfied. Simple examples show that a similar theorem is impossible in the node-capacitated setting. Nevertheless, we prove that an approximate flow/cut theorem does hold: For some universal c > 0, if the node cut conditions are satisfied, then one can simultaneously route a c-fraction of all the demands.

This answers an open question of Chekuri and Kawarabayashi. More generally, we show that this holds in the setting of multi-commodity polymatroid networks introduced by Chekuri, et. al. Our approach employs a new type of random metric embedding in order to round the convex programs corresponding to these more general flow problems.

For two metric spaces $X$ and $Y$, say that $X$ threshold-embeds into $Y$ if there exist a number $K > 0$ and a family of Lipschitz maps $\{\varphi_{\tau} : X \to Y : \tau > 0 \}$ such that for every $x,y \in X$, \[d_X(x,y) \geq \tau \implies d_Y(\varphi_{\tau}(x),\varphi_{\tau}(y)) \geq \|\varphi_{\tau}\|_{\mathrm{Lip}} \frac{\tau}{K},\] where $\|\varphi_{\tau}\|_{\mathrm{Lip}}$ denotes the Lipschitz constant of $\varphi_{\tau}$.

We show that if a metric space $X$ threshold-embeds into a Hilbert space, then $X$ has Markov type 2. As a consequence, planar graph metrics and doubling metrics have Markov type 2, answering questions of Naor, Peres, Schramm, and Sheffield. More generally, if a metric space $X$ threshold-embeds into a $p$-uniformly smooth Banach space, then $X$ has Markov type $p$. Our results suggest some non-linear analogs of Kwapien’s theorem. For instance, a subset $X \subseteq L_1$ threshold-embeds into Hilbert space if and only if $X$ has Markov type 2.

The $2$-sum embedding conjecture (Lee-Sidiropoulos, FOCS 2009) states that all the shortest-path metrics supported on a family of graphs $\mathcal F$ admit a uniformly bi-Lipschitz embedding into $L_1$ if and only if the same property holds for the closure of $\mathcal F$ under edge sums. The problem has an equivalent formulation in terms of multi-commodity flow/cut gaps and appears to be a fundamental step in resolving the well-studied question of which families of graphs admit an approximate multi-commodity max-flow/min-cut theorem.

The $2$-sum conjecture is known to be true when $\mathcal F = {K_3}$, where $K_n$ denotes the complete graph on $n$ vertices; this is equivalent to the seminal result of Gupta, Newman, Rabinovich, and Sinclair (Combinatorica, 2004) on embeddings of series-parallel graphs into $L_1$. For $\mathcal F = {K_4}$, the conjecture was confirmed by Chakrabarti, Jaffe, Lee, and Vincent (FOCS 2008). In the present paper, we prove the conjecture holds for any finite family of graphs $\mathcal F$. In fact, we obtain a quantitatively optimal result: Any path metric on a graph formed by $2$-sums of arbitrarily many copies of $K_n$ embeds into $L_1$ with distortion $O(\log n)$. This is a consequence of a more general theorem that characterizes the $L_1$ distortion of the 2-sum closure of any family $\mathcal F$ in terms of constrained embeddings of the members of $\mathcal F$.

For every \(\varepsilon > 0\), any subset of \(\mathbb{R}^n\) with Hausdorff dimension larger than \((1-\varepsilon) n\) must have ultrametric distortion larger than \(1/(4\varepsilon)\).

A basic fact in spectral graph theory is that the number of connected components in an undirected graph is equal to the multiplicity of the eigenvalue zero in the Laplacian matrix of the graph. In particular, the graph is disconnected if and only if there are at least two eigenvalues equal to zero. Cheeger’s inequality and its variants provide a robust version of the latter fact; they state that a graph has a sparse cut if and only if there are at least two eigenvalues that are close to zero.

It has been conjectured that an analogous characterization holds for higher multiplicities: There are k eigenvalues close to zero if and only if the vertex set can be partitioned into k subsets, each defining a sparse cut. We resolve this conjecture positively. Our result provides a theoretical justification for clustering algorithms that use the bottom k eigenvectors to embed the vertices into \(\mathbb{R}^k\), and then apply geometric considerations to the embedding. We also show that these techniques yield a nearly optimal quantitative connection between the expansion of sets of measure ≈ 1/k and the kth smallest eigenvalue of the normalized Laplacian.

Notes: A no frills proof of the higher-order Cheeger inequality
Related: One hundred hours of lectures from the SGT program at the Simons Institute.
Related: Laurent Miclo uses the higher-order Cheeger inequality for the basis of his resolution of Hoegh-Krohn and Simon’s conjecture that every hyperbounded operator has a spectral gap.

We show that every $n$-point tree metric admits a $(1+\varepsilon)$-bi-Lipschitz embedding into a $C(\varepsilon) \log n$-dimensional $\ell_1$ space for every $\varepsilon > 0$, where $C(\varepsilon) \leq O((1/\varepsilon)^4 \log (1/\varepsilon))$. This matches the natural volume lower bound up to a factor depending only on $\varepsilon$. Previously this was unknown even for complete binary trees.

(Mostly) expository note on Margulis-style expanders and their analysis. Significantly simpler than some previous analyses.

We show that the cover time of a graph can be related to the square of the maximum of the associated Gaussian free field. This yields a positive answer to a question of Aldous and Fill (1994) on deterministic approximations to the cover time, and positively resolves the Blanket Time conjecture of Winkler and Zuckerman (1996).

Video: Cover times of graphs and the Gaussian free field (Newton Institute)
Notes: Majorizing measures and Gaussian processes
Related questions and conjectures (all solved except the one after Lemma 4)

See also the related preprint of Alex Zhai that resolves our main conjecture.

We show that there is a family of $n$-point uniformly doubling metrics that require bilipschitz distortion $\Omega\left(\sqrt{\frac{\log n}{\log \log n}}\right)$ under any embedding into $L_1$, matching the known upper bound to within an $O(\sqrt{\log \log n})$ factor.

We prove diffusive lower bounds on the rate of escape of the random walk on infinite transitive graphs. Similar estimates hold for finite graphs, up to the relaxation time of the walk. Our approach uses nonconstant equivariant harmonic mappings taking values in a Hilbert space. For the special case of discrete, amenable groups, we present a more explicit proof of the Mok-Korevaar-Schoen theorem on the existence of such harmonic maps by constructing them from the heat flow on a Folner set.

We show there exists a metric space $(X,d)$ such that $(X,\sqrt{d})$ admits a bilipschitz embedding into $L_2$, but $(X,d)$ does not admit an equivalent metric of negative type. In fact, we exhibit a strong quantitative bound: There are $n$-point subsets $Y_n \subseteq X$ such that any mapping of $(Y_n,d)$ to a metric of negative type incurs distortion at least $\tilde{\Omega}(\log n)^{1/4}$.

This answers an open question about the strength of strong vs. weak triangle inequalities in a number of semidefinite programs. Our construction sheds light on the power of various notions of “dual flows” that arise in algorithms for approximating the Sparsest Cut problem. It also has other interesting implications for bilipschitz embeddings of finite metric spaces.

We show that every graph of pathwidth $k$ embeds into a distribution over random trees with distortion $c(k)$. In particular, this implies that whenever a non-trivial minor-closed family $\mathcal{F}$ of graphs does not contain all trees, the multi-commodity max-flow/min-cut gap is uniformly bounded for all instances over $\mathcal{F}$.

We show that for every $\alpha > 0$, there is an $n$-point metric space $(X,d)$ where every “scale” admits a Euclidean embedding with distortion at most $\alpha$, but any bi-Lipschitz embedding requires distortion $\Omega(\sqrt{\alpha \log n})$.

The matching upper bound was known to be tight at both endpoints (when $\alpha \asymp 1$ and $\alpha \asymp \log n$, but nowhere in between). This also shows that the “measured descent” method has an optimal asymptotic dependence on the parameters.

We study the quantitative geometry of graphs in terms of their genus, using the structure of certain cut graphs. These are subgraphs whose removal leaves a planar graph.

Indyk and Sidiropoulos (2007) proved that any orientable graph of genus $g$ can be probabilistically embedded into a graph of genus $g−1$ with constant distortion. Viewing a graph of genus $g$ as embedded on the surface of a sphere with $g$ handles attached, Indyk and Sidiropoulos’ method gives an embedding into a distribution over planar graphs with distortion $O(g)$ by iteratively removing the handles. By removing all g handles at once, we present a probabilistic embedding with distortion $O(g^2)$ for both orientable and non-orientable graphs. Our result is obtained by showing that the nimum-cut graph of Erickson and Har Peled (2004) has low dilation, and then randomly cutting this graph out of the surface using the Peeling Lemma of Lee and Sidiropoulos (2009).

We present a method for proving upper bounds on the eigenvalues of the graph Laplacian. A main step involves choosing an appropriate “Riemannian” metric to uniformize the geometry of the graph. In many interesting cases, the existence of such a metric is shown by examining the combinatorics of special types of flows. This involves proving new inequalities on the crossing number of graphs.

We use our method to show that for any positive integer k, the kth smallest eigenvalue of the Laplacian on an n-vertex, bounded-degree planar graph is O(k/n). This bound is asymptotically tight for every k, as it is easily seen to be achieved for square planar grids. We also extend this spectral result to graphs with bounded genus, and graphs which forbid fixed minors. Previously, such spectral upper bounds were only known for the case k=2.

A method is presented for establishing an upper bound on the first non-trivial eigenvalue of the Laplacian of a finite graph. Our approach uses multi-commodity flows to deform the geometry of the graph, and the resulting metric is embedded into Euclidean space to recover a bound on the Rayleigh quotient.

Using this, we resolve positively a question of Spielman and Teng by proving that \(\lambda_2(G) \leq O(d h^6 \log h/n)\) whenever \(G\) is a \(K_h\)-minor-free graph with maximum degree \(d\). While the standard “sweep” algorithm applied to the second eigenvector of a graph my fail to find a good quotient cut in graphs of unbounded degree, the arguments here produce a vector that works for arbitrary graphs. This yields an alterante proof of the Alon-Seymour-Thomas theorem that every excluded-minor family of graphs has \(O(\sqrt{n})\)-node balanced separators.

Related: These methods are extended to higher eigenvalues in a joint work with Kelner, Price, and Teng.
Related: These method form the basis for the uniformization and heat kernel bounds in Conformal growth rates and spectral geometry on distributional limits of graphs.

We initiate a systematic study of eigenvectors of random graphs. Whereas much is known about eigenvalues of graphs and how they reflect properties of the underlying graph, relatively little is known about the corresponding eigenvectors. Our main focus in this paper is on the nodal domains associated with the different eigenfunctions. In the analogous realm of Laplacians of Riemannian manifolds, nodal domains have been the subject of intensive research for well over a hundred years. Graphical nodal domains turn out to have interesting and unexpected properties.

Our main theorem asserts that there is a constant c such that for almost every graph G, each eigenfunction of G has at most two large nodal domains, and in addition at most c exceptional vertices outside these primary domains. We also discuss variations of these questions and briefly report on some numerical experiments which, in particular, suggest that almost surely there are just two nodal domains and no exceptional vertices.

Let $G$ be a finite group with symmetric generating set $S$, and let $c = \max_{R > 0} |B(2R)|/|B(R)|$ be the doubling constant of the corresponding Cayley graph, where $B(R)$ denotes an $R$-ball in the word-metric with respect to $S$. We show that the multiplicity of the $k$th eigenvalue of the Laplacian on the Cayley graph of $G$ is bounded by a function of only $c$ and $k$. More specifically, the multiplicity is at most $\exp((\log c)(\log c + \log k))$. Similarly, if $X$ is a compact, $n$-dimensional Riemannian manifold with non-negative Ricci curvature, then the multiplicity of the $k$th eigenvalue of the Laplace-Beltrami operator on $X$ is at most $\exp(n^2 + n \log k)$.

The first result (for $k=2$) yields the following group-theoretic application. There exists a normal subgroup $N$ of $G$, with $[G : N] \leq \alpha(c)$, and such that $N$ admits a homomorphism onto the cyclic group $Z_M$, where $M \geq |G|^{\delta(c)}$ and $\alpha(c), \delta(c) > 0$ are explicit functions depending only on $c$. This is the finitary analog of a theorem of Gromov which states that every infinite group of polynomial growth has a subgroup of finite index which admits a homomorphism onto the integers.

This addresses a question of Trevisan, and is proved by scaling down Kleiner’s proof of Gromov’s theorem. In particular, we replace the space of harmonic functions of fixed polynomial growth by the second eigenspace of the Laplacian on the Cayley graph of $G$.

We establish that the multi-commodity max-flow/min-cut gap for series-parallel graphs is at least $2$. Our approach uses the coarse differentiation methodology of Eskin, Fisher, and Whyte.

We give an explicit construction of subspaces $X \subseteq \mathbb{R}^N$ of dimension $(1-o(1)) N$ such that for every $x \in X$,

Through known connections between such Euclidean sections of $\ell_1$ and compressed sensing matrices, our result also gives explicit compressed sensing matrices for low compression factors for which basis pursuit is guaranteed to recover sparse signals. Our construction makes use of unbalanced bipartite graphs to impose local linear constraints on vectors in the subspace, and our analysis relies on expansion properties of the graph. This is inspired by similar constructions of error-correcting codes.

We show that an infinite weighted tree admits a bi-Lipschitz embedding into Hilbert space if and only if it does not contain arbitrarily large complete binary trees with uniformly bounded distortion. We also introduce a new metric invariant called Markov convexity, and show how it can be used to compute the Euclidean distortion of any metric tree up to universal factors.

We consider questions about vertex cuts in graphs, random walks in metric spaces, and dimension reduction in $\ell_1$ and $\ell_2$; these topics are intimately connected because they can each be reduced to the existence of various families of real-valued Lipschitz maps on certain metric spaces. We view these issues through the lens of shortest-path metrics on series-parallel graphs, and we discuss the implications for a variety of well-known open problems.

It is well-known that $\mathbb{R}^N$ has has subspaces of dimension proportional to $N$ on which the $\ell_1$ and $\ell_2$ norms are uniformly equivalent, but it is unknown how to construct them explicitly. We show that, for any $\delta > 0$, such a subspace can be generated using only $N^{\delta}$ random bits. This improves over previous constructions of Artstein-Avidan and Milman, and of Lovett and Sodin, which require $O(N log N)$, and $O(N)$ random bits, respectively.

It is known that such subspaces give rise to error-correcting codes over the reals and compressed sensing matrices. As in the work of Guruswami, Lee, and Razborov, our construction is the continuous analog of a Tanner code, and makes use of expander graphs to impose a collection of local linear constraints on vectors in the subspace. Our analysis is able to achieve uniform equivalence of the $\ell_1$ and $\ell_2$ norms (independent of the dimension). It has parallels to iterative decoding of Tanner codes, and leads to an analogous near-linear time algorithm for error-correction over reals.

We prove that the function \(d : \mathbb{R}^3 \times \mathbb{R}^3 \to [0,\infty)\) given by

is a metric on \(\mathbb{R}^3\) such that \((\mathbb{R}^3, \sqrt{d})\) is isometric to a subset of Hilbert space, yet \((\mathbb{R}^3,d)\) does not admit a bi-Lipschitz embedding into \(L_1\). This yields a new simple counter example to the Goemans-Linial conjecture on the integrality gap of the SDP relaxation of the Sparsest Cut problem.

Our methods involve Fourier analytic techniques, combined with a breakthrough of Cheeger and Kleiner, along with classical results of Pansu on the differentiability of Lispchitz functions on the Heisenberg group.

We present an $O(\sqrt{\log n} \log \log n)$ upper bound on the $(n-1)$-dimensional volume distortion of $n$-point subsets of a Euclidean space, nearly resolving the main open questions of [Dunagan-Vempala 2001] and [Krauthgamer-Linial-Magen 2004]. The best previous bound was $O(\log n)$ and our bound is nearly tight, as even the $2$-dimensional volume distortion of an $n$-vertex path is $\Omega(\sqrt{\log n})$.

We explore approximation algorithms on negatively curved metric spaces in the sense of Gromov. For instance, we show that the Traveling Salesman Problem admits a PTAS when the set of points lies in hyperbolic $d$-space.

We observe that combining the techniques behind the Sparsest Cut SDP analysis of Arora, Rao, and Vazirani, with the rounding algorithm of Rao and Richa yields an $O(\sqrt{\log n} \log \log n)$-approximation for the minimum linear arrangement problem, improving over the previous bound of $O(\log n)$.

This paper strengthens the main result of Euclidean distortion and the Sparsest Cut by showing that one can use a Fréchet embedding.

We prove that every \(n\)-point metric space of negative type (and, in particular, every \(n\)-point subset of \(L_1\)) embeds into a Euclidean space with distortion \(O(\sqrt{\log n} \log \log n)\), a result which is tight up to the iterated logarithm factor. As a consequence, we obtain the best known polynomial-time approximation algorithm for the Sparsest Cut problem with general demands. If the demand is supported on a set of size \(k\), we achieve an approximation ratio of \(O(\sqrt{\log k} \log \log k)\).

We develop the algorithmic theory of vertex separators, and its relation to embeddings of certain metric spaces. As a consequence, we obtain an \(O(\sqrt{\log n})\)-approximation for min-ratio vertex cuts in general graphs based on a new SDP relaxation and a tight analysis of its integrality gap.

Our results allow yield algorithms for constructing approximately optimal tree decompositions of graphs. If a graph has treewidth \(k\), we find a tree decomposition of width at most \(O(k \sqrt{\log k})\). If, additionally, the input graph excludes a fixed graph as a minor, we produce a tree decomposition of width \(O(k)\).

Related: A similar method gives improved bounds for the minimum linear arrangement problem.

[Note: This is the (unpublished) full version of a paper appearing in the SODA 2005 conference under the name Distance scales, embeddings, and efficient relaxations of the cut cone.]

We introduce a new number of new techniques for the construction of low-distortion embeddings of a finite metric space. These include a generic Gluing Lemma which avoids the overhead typically incurred from the naı̈ve concatenation of maps for different scales of a space. We also give a significantly improved and quantitatively optimal version of the main structural theorem of Arora, Rao, and Vazirani on separated sets in metrics of negative type. The latter result offers a simple hyperplane rounding algorithm for the computation of an \(O(\sqrt{\log n})\)-approximation to the Sparsest Cut problem with uniform demands, and has a number of other applications to embeddings and approximation algorithms.

For a more elegant and simpler proof of the “Big Core” Theorem, one can consult these notes of Rothvoss.

We present some new observations concerning the relation of finite subsets of $L_1$ to dimension reduction, topology, and Euclidean distortion.

We develop here a new multi-scale embedding method that we term measured descent and use it to resolve a number of open questions in the theory of embeddings of finite metric spaces.

Many classical problems in geometry and analysis involve the gluing together of local information to produce a coherent global picture. Inevitably, the difficulty of such a procedure lies at the local boundary, where overlapping views of the same locality must somehow be merged. It is therefore desirable that the boundaries be “smooth,” allowing a graceful transition from one viewpoint to the next. For instance, one may point to Whitney’s use of partitions of unity in studying what is now known as the Whitney extension problem.

In the present work, we consider what is perhaps the most basic Whitney-type extension problem, that of extending a Lipschitz function so that it remains Lipschitz. Often such a map is extended by first producing a cover of the new domain, extending the mapping locally, and then gluing together the individual pieces. Our main observation is that in many cases, if one chooses a random cover from the right distribution, the boundary can be made “smooth” on average, even when the local maps are individually quite coarse. This insight leads to the unification, generalization, and improvement of many known results, as well as to new results for many interesting spaces.

This paper establishes that a metric space $X$ supports approximate nearest-neighbor queries against any $n$-point subset with at most $\mathrm{poly}(\log n)$ query time if and only if one has certain quantitative estimates on the doubling constant of $n$-point subsets.

Announcement of Extending Lipschitz functions via random metric partitions.

We present simple deterministic data structures for maintaining a set of points in a metric space under insertions and deletions, with the ability to make fast nearest-neighbor queries. The running-time of the operations scales with the doubling constant of the underlying metric space.

We show that every embedding of the level $k$ diamond graph of Newman and Rabinovich into $L_p$ with $1 < p \leq 2$ requires distortion at least $\sqrt{k(p-1)+1}$. An immediate corollary is that there exist arbitrary large $n$-point subsets $X \subseteq L_1$ such that any $D$-embedding of $X$ into $\ell_1^d$ requires $d \geq n^{\Omega(1/D^2)}$. This gives a simple proof of the $L_1$ dimension reduction lower bound of Brinkman and Charikar.

We study the quantitative ditsortion required to embed finite, uniformly doubling metric spaces into normed spaces.

We resolve a conjecture of Levin together with Linial, London, and Rabinovich about embeddings of graphs whose intrinsic metric has polynomial growth. We also resolve positively a related embedding question of Benjamini and Schramm.

We establish lower bounds on the polynomial-time approximability of the vertex-connectivity variant of the Survivable Network Design Problem (SNDP) under the assumption that \(\mathsf{NP}\) does not have quasipolynomial-time algorithms. Some related hardness of approximation results are established, e.g., for the edge and vertex-connectivity augmention problems.