First, some definitions:

Lipschitz continuity

$\newcommand{\norm}[1]{\left\| #1\right\|}$ A function $f$ is called L-Lipschitz over a set S with respect to a norm $\norm{·}$ if for all $u,w \in S$ we have:

$$\begin{equation} \left|f(u) − f(w)\right| \leq L\norm{u − w}. \end{equation}$$

Some people will equivalently say $f$ is Lipschitz continuous with Lipschitz constant $L$.
Intuitively, $L$ is a measure of how fast the function can change.

Convexity, subgradients

function is convex if :

$$f((1-\alpha) a+ \alpha b) \leq (1-\alpha ) f(a)+\alpha f(b) \quad \forall a,b, \quad 0 \le \alpha \le 1$$

In a picture, the line between two points is an upper bound on the function evaluated at any point in the line. Here we see an example for $f(x) = x^2$, $a = -1$, $b = 1.5$. Compare it to concave functions.

An equivalent definition of a convex function is that $\forall w, u \in \mathbb{R}^n, \exists g \in \mathbb{R}^{n}$ such that:

$$f(u) \geq f(w) + \langle g, (u-w) \rangle \quad (1)$$

In this case, we have that $\hat{f}(u) = f(w) + \langle g, (u-w) \rangle$ is a linear lower bound for the function, which is tight at $w$ Here we see a example in 1 dimension for $f(x) = x^2$, $w = 1$, $g = 2$.

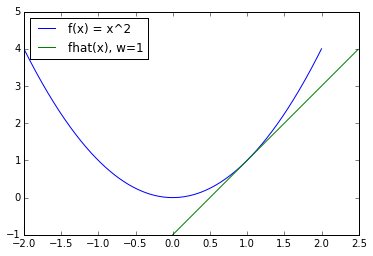
Subgradients

• $g$ is a subgradient of $f$ at $w$ if inequality (1) holds.
• $\partial f(w)$ is the subdifferential of $f$ at $w$, or set of subgradients of $f$ at $w$
• If $f$ is differentiable, $\partial f(w) = \{\nabla f(w)\}$.

Relationship between Lipschitz constant and norm of subgradients

There is a nice Lemma (2.6 from this survey) that relates L to the norm of the subgradients of $f$. It states the following:
Let $f$ be a convex function. Then, $f$ is L-Lipschitz over $S$ with respect to norm $\norm{.}$ if and only if for all $w \in S$ and $z \in \partial f(w)$ we have that $\norm{z}_{*} \leq L$, where $\norm{.}_{*}$ is the dual norm.

In other words, Lipschitz continuity over some norm implies a bound on the dual norm of the subgradients (and thus the gradients, if the function is differentiable) of the function - and vice versa.
First, we will prove this bound. Then, we will give examples of its applications to some functions and intuition.

Proof (from the survey): Assume that $f$ is L-Lipschitz. Choose some $w \in S$, $z \in \partial f(w)$.
Let $u - w =argmax_{v:\norm{v} = 1} \langle v, z \rangle$. Note that by definition, $\langle u-w, z \rangle = \norm{z}_{*}$. Also note that $\norm{u-w} = 1$, by the way we defined it.
From the definition of subgradient, we have the following inequality:

$$f(u) - f(w) \geq \underbrace{\langle z, u-w \rangle}_{\norm{z}_{*}}$$

Since we assume that $f$ is Lipschitz continuous, we have:

$$L\underbrace{\norm{u-w}}_{=1} \geq f(u) - f(w)$$

Combining the above two inequalities, we conclude that if $f$ is L-Lipschitz, $L \geq \norm{z}_{*}$.

Now we prove the other direction (if $L \geq \norm{z}_{*}$, $f$ is L-Lipschitz). We now use the definition of subgradient again, multiplied by -1:

$$f(w) - f(u) \leq \langle z, (w-u) \rangle$$

Combining this with the general dual norm result that $\langle w,z \rangle \leq \norm{w}\norm{z}_{*}$, we get:

$$f(w) - f(u) \leq \norm{w -u}\underbrace{\norm{z}_{*}}_{\leq L} \leq L \norm{w -u}$$

Which by definition means that $f$ is L-lipschitz.

This gives us intuition about Lipschitz continuous convex functions: their gradients must be bounded, so that they can't change too much too quickly.

Examples

We now provide some example functions. Lets assume we are using the L2 norm. First, Lets look at $f(x) = \dfrac{x^2}{3}$:

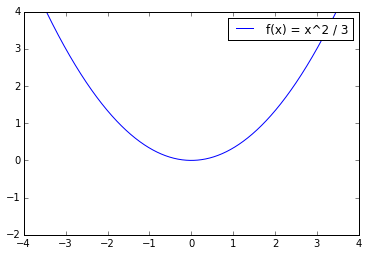
Is it Lipschitz continous? This function happens to be differentiable, so we have that $\partial f(x) = \{\nabla f(x) = \dfrac{2x}{3}\}$ Clearly, the subgradients are not bounded (they go to infinity as $x$ goes to infinity), so this function is NOT Lipschitz continuous. Intuitively, as $x$ grows, the change in the $y$ axis grows faster and faster, much faster than the change in the x axis times some constant. Is the gradient of $f(x)$ Lipschitz continuous? Well, the subgradient of the gradient is $\dfrac{2}{3}$, so it is clearly bounded. Thus, we conclude that the gradient of $f(x)$ is Lipschitz continuous with $L = \dfrac{2}{3}$.

Now, let $f(x) = \left \vert x \right \vert$:

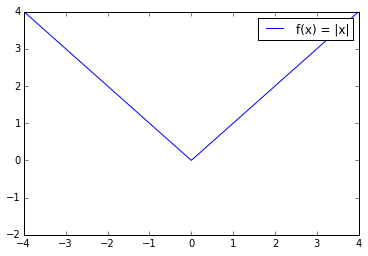
In this case, it is easy to see that the subgradient is $g = -1$ from $(-\infty, 0)$, $g \in (-1, 1)$ at 0 and $g = 1$ from $(0, +\infty)$. From the theorem, we conclude that the function is Lipchitz continuous with $L=1$. The gradient is not continuous, so it is also not Lipschitz Continuous (the gradient at the point of discontinuity would be infinite).