Publications

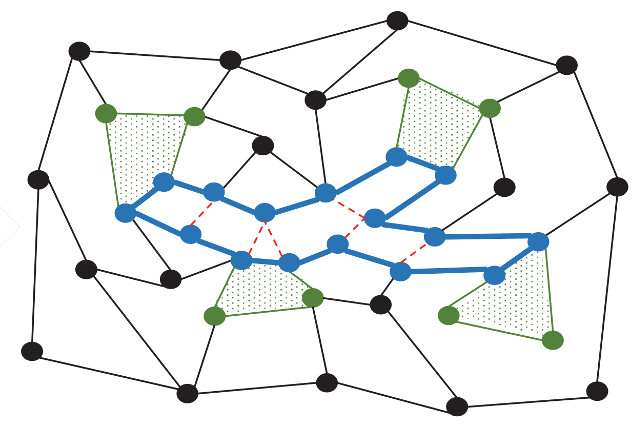
We establish new and improved bounds on the flow-cut gap in planar flow networks where the terminals lie on a small number of faces. The classical Okamura-Seymour theorem (1981) shows that when all terminals lie on a single face, the flow-cut gap is exactly 1. We show that if the terminals lie on $\gamma$ faces, the flow-cut gap is $O(\log \gamma)$. This is proved by embedding the terminal metric into a distribution over trees with distortion $O(\log \gamma)$, which is tight up to the implied constant factor.

A region intersection graph over a base graph \(G_0\) is a graph \(G\) whose vertices correspond to connected subsets of \(G_0\) with an edge between two vertices if the corresponding regions intersect. We show that if \(G_0\) excludes the complete graph \(K_h\) as a minor, then every region intersection graph over \(G_0\) with m edges has a balanced separator with \(O(\sqrt{m})\) nodes. If \(G\) has uniformly bounded vertex degrees, we show the separator is found by spectral partitioning.

A string graph is the intersection graph of continuous arcs in the plane. The preceding result implies that every string graph with m edges has a balanced separator of size \(O(\sqrt{m})\). This bound is optimal, as it generalizes the planar separator theorem. It confirms a conjecture of Fox and Pach (2010) and improves over the \(O(\sqrt{m} \log m)\) bound of Matousek (2013).

The classical Okamura-Seymour theorem states that for an edge-capacitated, multi-commodity flow instance in which all terminals lie on a single face of a planar graph, there exists a feasible concurrent flow if and only if the cut conditions are satisfied. Simple examples show that a similar theorem is impossible in the node-capacitated setting. Nevertheless, we prove that an approximate flow/cut theorem does hold: For some universal c > 0, if the node cut conditions are satisfied, then one can simultaneously route a c-fraction of all the demands.

This answers an open question of Chekuri and Kawarabayashi. More generally, we show that this holds in the setting of multi-commodity polymatroid networks introduced by Chekuri, et. al. Our approach employs a new type of random metric embedding in order to round the convex programs corresponding to these more general flow problems.

The $2$-sum embedding conjecture (Lee-Sidiropoulos, FOCS 2009) states that all the shortest-path metrics supported on a family of graphs $\mathcal F$ admit a uniformly bi-Lipschitz embedding into $L_1$ if and only if the same property holds for the closure of $\mathcal F$ under edge sums. The problem has an equivalent formulation in terms of multi-commodity flow/cut gaps and appears to be a fundamental step in resolving the well-studied question of which families of graphs admit an approximate multi-commodity max-flow/min-cut theorem.

The $2$-sum conjecture is known to be true when $\mathcal F = {K_3}$, where $K_n$ denotes the complete graph on $n$ vertices; this is equivalent to the seminal result of Gupta, Newman, Rabinovich, and Sinclair (Combinatorica, 2004) on embeddings of series-parallel graphs into $L_1$. For $\mathcal F = {K_4}$, the conjecture was confirmed by Chakrabarti, Jaffe, Lee, and Vincent (FOCS 2008). In the present paper, we prove the conjecture holds for any finite family of graphs $\mathcal F$. In fact, we obtain a quantitatively optimal result: Any path metric on a graph formed by $2$-sums of arbitrarily many copies of $K_n$ embeds into $L_1$ with distortion $O(\log n)$. This is a consequence of a more general theorem that characterizes the $L_1$ distortion of the 2-sum closure of any family $\mathcal F$ in terms of constrained embeddings of the members of $\mathcal F$.

We show that there is a family of $n$-point uniformly doubling metrics that require bilipschitz distortion $\Omega\left(\sqrt{\frac{\log n}{\log \log n}}\right)$ under any embedding into $L_1$, matching the known upper bound to within an $O(\sqrt{\log \log n})$ factor.

We show there exists a metric space $(X,d)$ such that $(X,\sqrt{d})$ admits a bilipschitz embedding into $L_2$, but $(X,d)$ does not admit an equivalent metric of negative type. In fact, we exhibit a strong quantitative bound: There are $n$-point subsets $Y_n \subseteq X$ such that any mapping of $(Y_n,d)$ to a metric of negative type incurs distortion at least $\tilde{\Omega}(\log n)^{1/4}$.

This answers an open question about the strength of strong vs. weak triangle inequalities in a number of semidefinite programs. Our construction sheds light on the power of various notions of “dual flows” that arise in algorithms for approximating the Sparsest Cut problem. It also has other interesting implications for bilipschitz embeddings of finite metric spaces.

We show that every graph of pathwidth $k$ embeds into a distribution over random trees with distortion $c(k)$. In particular, this implies that whenever a non-trivial minor-closed family $\mathcal{F}$ of graphs does not contain all trees, the multi-commodity max-flow/min-cut gap is uniformly bounded for all instances over $\mathcal{F}$.

We study the quantitative geometry of graphs in terms of their genus, using the structure of certain cut graphs. These are subgraphs whose removal leaves a planar graph.

Indyk and Sidiropoulos (2007) proved that any orientable graph of genus $g$ can be probabilistically embedded into a graph of genus $g−1$ with constant distortion. Viewing a graph of genus $g$ as embedded on the surface of a sphere with $g$ handles attached, Indyk and Sidiropoulos’ method gives an embedding into a distribution over planar graphs with distortion $O(g)$ by iteratively removing the handles. By removing all g handles at once, we present a probabilistic embedding with distortion $O(g^2)$ for both orientable and non-orientable graphs. Our result is obtained by showing that the nimum-cut graph of Erickson and Har Peled (2004) has low dilation, and then randomly cutting this graph out of the surface using the Peeling Lemma of Lee and Sidiropoulos (2009).

We present a method for proving upper bounds on the eigenvalues of the graph Laplacian. A main step involves choosing an appropriate “Riemannian” metric to uniformize the geometry of the graph. In many interesting cases, the existence of such a metric is shown by examining the combinatorics of special types of flows. This involves proving new inequalities on the crossing number of graphs.

We use our method to show that for any positive integer k, the kth smallest eigenvalue of the Laplacian on an n-vertex, bounded-degree planar graph is O(k/n). This bound is asymptotically tight for every k, as it is easily seen to be achieved for square planar grids. We also extend this spectral result to graphs with bounded genus, and graphs which forbid fixed minors. Previously, such spectral upper bounds were only known for the case k=2.

A method is presented for establishing an upper bound on the first non-trivial eigenvalue of the Laplacian of a finite graph. Our approach uses multi-commodity flows to deform the geometry of the graph, and the resulting metric is embedded into Euclidean space to recover a bound on the Rayleigh quotient.

Using this, we resolve positively a question of Spielman and Teng by proving that \(\lambda_2(G) \leq O(d h^6 \log h/n)\) whenever \(G\) is a \(K_h\)-minor-free graph with maximum degree \(d\). While the standard “sweep” algorithm applied to the second eigenvector of a graph my fail to find a good quotient cut in graphs of unbounded degree, the arguments here produce a vector that works for arbitrary graphs. This yields an alterante proof of the Alon-Seymour-Thomas theorem that every excluded-minor family of graphs has \(O(\sqrt{n})\)-node balanced separators.

Related: These methods are extended to higher eigenvalues in a joint work with Kelner, Price, and Teng.
Related: These method form the basis for the uniformization and heat kernel bounds in Conformal growth rates and spectral geometry on distributional limits of graphs.

We establish that the multi-commodity max-flow/min-cut gap for series-parallel graphs is at least $2$. Our approach uses the coarse differentiation methodology of Eskin, Fisher, and Whyte.

We develop the algorithmic theory of vertex separators, and its relation to embeddings of certain metric spaces. As a consequence, we obtain an \(O(\sqrt{\log n})\)-approximation for min-ratio vertex cuts in general graphs based on a new SDP relaxation and a tight analysis of its integrality gap.

Our results allow yield algorithms for constructing approximately optimal tree decompositions of graphs. If a graph has treewidth \(k\), we find a tree decomposition of width at most \(O(k \sqrt{\log k})\). If, additionally, the input graph excludes a fixed graph as a minor, we produce a tree decomposition of width \(O(k)\).

Related: A similar method gives improved bounds for the minimum linear arrangement problem.