Publications

In a hypergraph on $n$ vertices where $D$ is the maximum size of a hyperedge, there is a weighted hypergraph spectral $\varepsilon$-sparsifier with at most $O(\varepsilon^{-2} \log(D) \cdot n \log n)$ hyperedges. This improves over the bound of Kapralov, Krauthgamer, Tardos and Yoshida (2021) who achieve $O(\varepsilon^{-4} n (\log n)^3)$, as well as the bound $O(\varepsilon^{-2} D^3 n \log n)$ obtained by Bansal, Svensson, and Trevisan (2019).

Consider an infinite planar graph with uniform polynomial growth of degree $d > 2$. Many examples of such graphs exhibit similar geometric and spectral properties, and it has been conjectured that this is necessary. We present a family of counterexamples. In particular, we show that for every rational $d > 2$, there is a planar graph with uniform polynomial growth of degree $d$ on which the random walk is transient, disproving a conjecture of Benjamini (2011).

By a well-known theorem of Benjamini and Schramm, such a graph cannot be a unimodular random graph. We also give examples of unimodular random planar graphs of uniform polynomial growth with unexpected properties. For instance, graphs of (almost sure) uniform polynomial growth of every rational degree $d > 2$ for which the speed exponent of the walk is larger than $1/d$, and in which the complements of all balls are connected. This resolves negatively two questions of Benjamini and Papasoglou (2011).

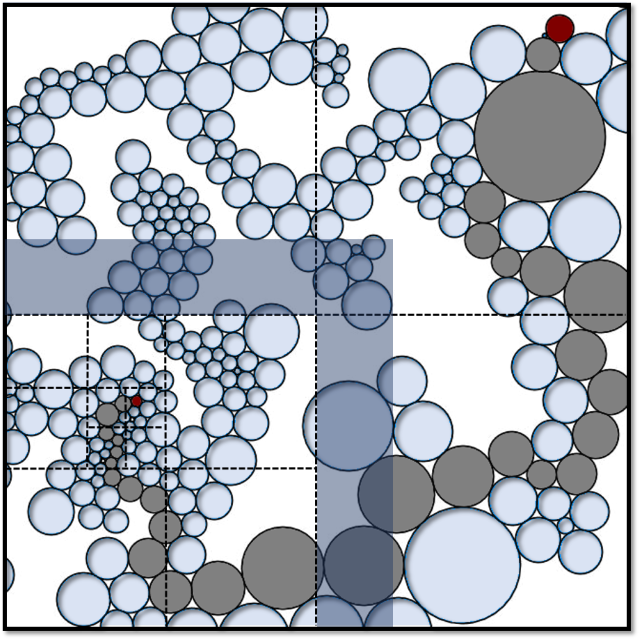
If \((G, \rho)\) is the distributional limit of finite graphs that can be sphere-packed in \(\mathbb{R}^d\), then the conformal growth exponent of \((G, \rho)\) is at most d. In other words, there exists a unimodular “unit volume” weighting of the graph metric on G such that the volume growth of balls is asymptotically polynomial with exponent d. This generalizes to graphs that can be quasisymmetrically packed in an Ahlfors d-regular metric measure space. Using our previous work, it gives bounds on the almost sure spectral dimension of G.

For a unimodular random graph \((G, \rho)\), we consider deformations of its intrinsic path metric by a (random) weighting of its vertices. This leads to the notion of the conformal growth exponent of \((G, \rho)\), which is the best asymptotic degree of volume growth of balls that can be achieved by such a weighting. Under moment conditions on the degree of the root, we show that the conformal growth exponent of a unimodular random graph bounds its almost sure spectral dimension.

For two-dimensional growth, one obtains more precise information about recurrence, the heat kernel, and subdiffusivity of the random walk. In particular, this gives a new method for studying the uniform infinite planar triangulation (UIPT) and quadrangulation (UIPQ).

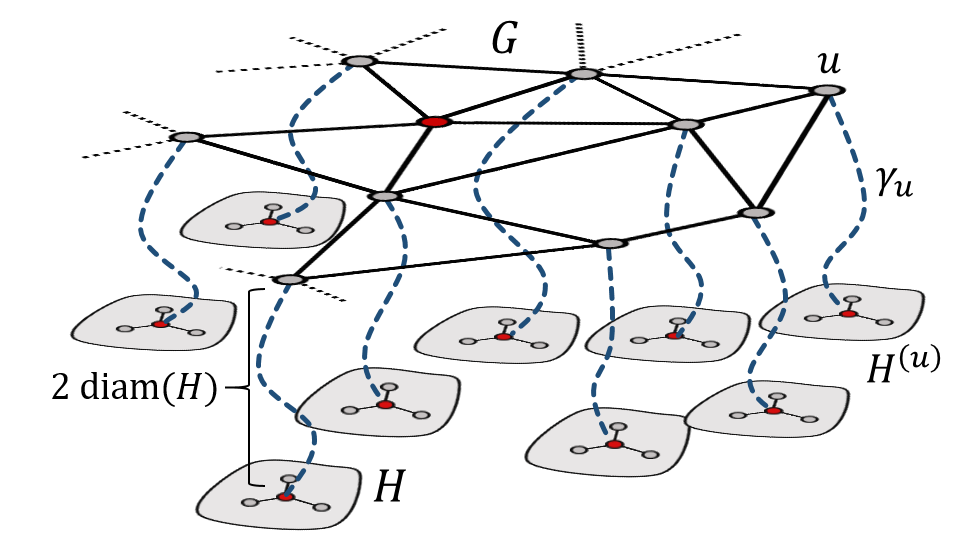
We show that if $(G,\rho)$ is a stationary random graph of annealed polynomial growth, then almost surely there is an infinite sequence of times at which the random walk started from x is at most diffusive. This result is new even in the case when G is a stationary random subgraph of $\mathbb{Z}^d$. Combined with the work of Benjamini, Duminil-Copin, Kozma, and Yadin, it implies that G almost surely does not admit a non-constant harmonic function of sublinear growth.

To complement this, we argue that passing to a subsequence of times is necessary, as there are stationary random graphs of (almost sure) polynomial growth where the random walk is almost surely superdiffisuve at an infinite subset of times.

Addendum: In the paper, we ask whether passing to a subsequence of times is necessary when $G$ is a stationary random subgraph of $\mathbb{Z}^d$. For the case $d=2$, it holds for all times using my paper with Ding and Peres. For $d$ sufficiently large, passing to a subsequence of times is necessary; this can be proved by showing that our stationary random graph occurs as a stationary random subgraph of $\mathbb{Z}^d_{\infty}$, using my paper with Krauthgamer.

A region intersection graph over a base graph \(G_0\) is a graph \(G\) whose vertices correspond to connected subsets of \(G_0\) with an edge between two vertices if the corresponding regions intersect. We show that if \(G_0\) excludes the complete graph \(K_h\) as a minor, then every region intersection graph over \(G_0\) with m edges has a balanced separator with \(O(\sqrt{m})\) nodes. If \(G\) has uniformly bounded vertex degrees, we show the separator is found by spectral partitioning.

A string graph is the intersection graph of continuous arcs in the plane. The preceding result implies that every string graph with m edges has a balanced separator of size \(O(\sqrt{m})\). This bound is optimal, as it generalizes the planar separator theorem. It confirms a conjecture of Fox and Pach (2010) and improves over the \(O(\sqrt{m} \log m)\) bound of Matousek (2013).

A basic fact in spectral graph theory is that the number of connected components in an undirected graph is equal to the multiplicity of the eigenvalue zero in the Laplacian matrix of the graph. In particular, the graph is disconnected if and only if there are at least two eigenvalues equal to zero. Cheeger’s inequality and its variants provide a robust version of the latter fact; they state that a graph has a sparse cut if and only if there are at least two eigenvalues that are close to zero.

It has been conjectured that an analogous characterization holds for higher multiplicities: There are k eigenvalues close to zero if and only if the vertex set can be partitioned into k subsets, each defining a sparse cut. We resolve this conjecture positively. Our result provides a theoretical justification for clustering algorithms that use the bottom k eigenvectors to embed the vertices into \(\mathbb{R}^k\), and then apply geometric considerations to the embedding. We also show that these techniques yield a nearly optimal quantitative connection between the expansion of sets of measure ≈ 1/k and the kth smallest eigenvalue of the normalized Laplacian.

Notes: A no frills proof of the higher-order Cheeger inequality
Related: One hundred hours of lectures from the SGT program at the Simons Institute.
Related: Laurent Miclo uses the higher-order Cheeger inequality for the basis of his resolution of Hoegh-Krohn and Simon’s conjecture that every hyperbounded operator has a spectral gap.

(Mostly) expository note on Margulis-style expanders and their analysis. Significantly simpler than some previous analyses.

We show that the cover time of a graph can be related to the square of the maximum of the associated Gaussian free field. This yields a positive answer to a question of Aldous and Fill (1994) on deterministic approximations to the cover time, and positively resolves the Blanket Time conjecture of Winkler and Zuckerman (1996).

Video: Cover times of graphs and the Gaussian free field (Newton Institute)
Notes: Majorizing measures and Gaussian processes
Related questions and conjectures (all solved except the one after Lemma 4)

See also the related preprint of Alex Zhai that resolves our main conjecture.

We prove diffusive lower bounds on the rate of escape of the random walk on infinite transitive graphs. Similar estimates hold for finite graphs, up to the relaxation time of the walk. Our approach uses nonconstant equivariant harmonic mappings taking values in a Hilbert space. For the special case of discrete, amenable groups, we present a more explicit proof of the Mok-Korevaar-Schoen theorem on the existence of such harmonic maps by constructing them from the heat flow on a Folner set.

We present a method for proving upper bounds on the eigenvalues of the graph Laplacian. A main step involves choosing an appropriate “Riemannian” metric to uniformize the geometry of the graph. In many interesting cases, the existence of such a metric is shown by examining the combinatorics of special types of flows. This involves proving new inequalities on the crossing number of graphs.

We use our method to show that for any positive integer k, the kth smallest eigenvalue of the Laplacian on an n-vertex, bounded-degree planar graph is O(k/n). This bound is asymptotically tight for every k, as it is easily seen to be achieved for square planar grids. We also extend this spectral result to graphs with bounded genus, and graphs which forbid fixed minors. Previously, such spectral upper bounds were only known for the case k=2.

A method is presented for establishing an upper bound on the first non-trivial eigenvalue of the Laplacian of a finite graph. Our approach uses multi-commodity flows to deform the geometry of the graph, and the resulting metric is embedded into Euclidean space to recover a bound on the Rayleigh quotient.

Using this, we resolve positively a question of Spielman and Teng by proving that \(\lambda_2(G) \leq O(d h^6 \log h/n)\) whenever \(G\) is a \(K_h\)-minor-free graph with maximum degree \(d\). While the standard “sweep” algorithm applied to the second eigenvector of a graph my fail to find a good quotient cut in graphs of unbounded degree, the arguments here produce a vector that works for arbitrary graphs. This yields an alterante proof of the Alon-Seymour-Thomas theorem that every excluded-minor family of graphs has \(O(\sqrt{n})\)-node balanced separators.

Related: These methods are extended to higher eigenvalues in a joint work with Kelner, Price, and Teng.
Related: These method form the basis for the uniformization and heat kernel bounds in Conformal growth rates and spectral geometry on distributional limits of graphs.

We initiate a systematic study of eigenvectors of random graphs. Whereas much is known about eigenvalues of graphs and how they reflect properties of the underlying graph, relatively little is known about the corresponding eigenvectors. Our main focus in this paper is on the nodal domains associated with the different eigenfunctions. In the analogous realm of Laplacians of Riemannian manifolds, nodal domains have been the subject of intensive research for well over a hundred years. Graphical nodal domains turn out to have interesting and unexpected properties.

Our main theorem asserts that there is a constant c such that for almost every graph G, each eigenfunction of G has at most two large nodal domains, and in addition at most c exceptional vertices outside these primary domains. We also discuss variations of these questions and briefly report on some numerical experiments which, in particular, suggest that almost surely there are just two nodal domains and no exceptional vertices.

Let $G$ be a finite group with symmetric generating set $S$, and let $c = \max_{R > 0} |B(2R)|/|B(R)|$ be the doubling constant of the corresponding Cayley graph, where $B(R)$ denotes an $R$-ball in the word-metric with respect to $S$. We show that the multiplicity of the $k$th eigenvalue of the Laplacian on the Cayley graph of $G$ is bounded by a function of only $c$ and $k$. More specifically, the multiplicity is at most $\exp((\log c)(\log c + \log k))$. Similarly, if $X$ is a compact, $n$-dimensional Riemannian manifold with non-negative Ricci curvature, then the multiplicity of the $k$th eigenvalue of the Laplace-Beltrami operator on $X$ is at most $\exp(n^2 + n \log k)$.

The first result (for $k=2$) yields the following group-theoretic application. There exists a normal subgroup $N$ of $G$, with $[G : N] \leq \alpha(c)$, and such that $N$ admits a homomorphism onto the cyclic group $Z_M$, where $M \geq |G|^{\delta(c)}$ and $\alpha(c), \delta(c) > 0$ are explicit functions depending only on $c$. This is the finitary analog of a theorem of Gromov which states that every infinite group of polynomial growth has a subgroup of finite index which admits a homomorphism onto the integers.

This addresses a question of Trevisan, and is proved by scaling down Kleiner’s proof of Gromov’s theorem. In particular, we replace the space of harmonic functions of fixed polynomial growth by the second eigenspace of the Laplacian on the Cayley graph of $G$.