Continuous-time Value Function Approximation in Reproducing Kernel Hilbert Spaces
We proposed a reinforcement learning technique working in reproducing kernel Hilbert spaces for systems described by stochastic differential equations.
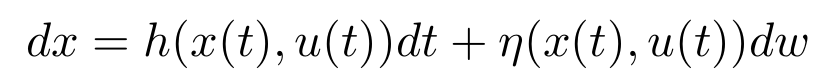
Theoretically, the proposed framework is based on a one-to-one mapping between the RKHS for the value function and that for the immediate reward function. (We also showed that the proposed framework also reproduces some of the existing kernel-based discrete-time RL techniques)
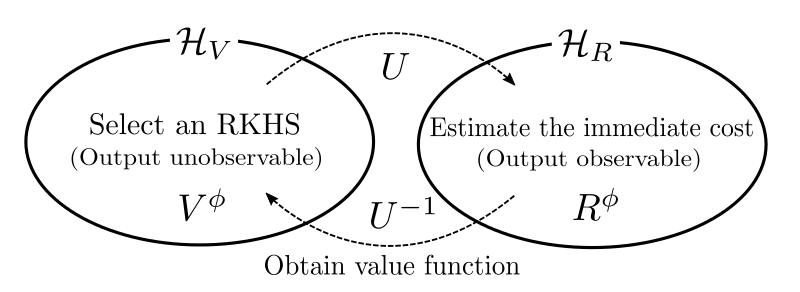
We showed that the continuous-time formulation is methodologically more desirable over the discrete-time formulation in terms of affinity for the control theory and susceptibility to numerical errors.