Online Nonlinear Estimation via Iterative L2-Space Projections: Reproducing Kernel of Subspace
This work began with the question: Should we always select reproducing kernel Hilbert spaces for efficiently conducting adaptive nonlinear estimation?
We proposed a novel nonlinear estimation technique working in the L2 space to speed-up learning.

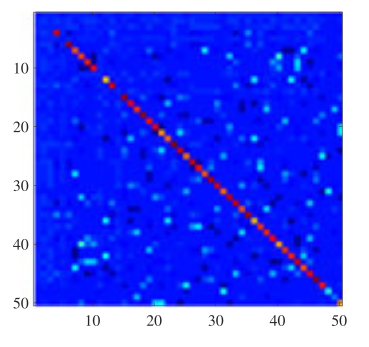
This work showed importance of properly selecting metric for nonlinear estimation tasks. (For nonlinear estimation tasks, one needs to consider a Hilbert space of infinite dimension, which is not necessarily an RKHS) The figure below shows that the autocorrelatin matrix of the input vector transformed to the L2 space is close to the identity matrix.
The proposed algorithms were compared with a bunch of machine learning batch methods and the Extended Kalman Filter.