Publications

We consider the sparsification of sums \(F : \mathbb{R}^n \to \mathbb{R}_+\) where \(F(x) = f_1(\langle a_1,x\rangle) + \cdots + f_m(\langle a_m,x\rangle)\) for vectors $a_1,\ldots,a_m \in \mathbb{R}^n$ and functions $f_1,\ldots,f_m : \mathbb{R} \to \mathbb{R}_+$. We show that $(1+\varepsilon)$-approximate sparsifiers of $F$ with support size $\frac{n}{\varepsilon^2} (\log \frac{n}{\varepsilon})^{O(1)}$ exist whenever the functions $f_1,\ldots,f_m$ are symmetric, monotone, and satisfy natural growth bounds. Additionally, we give efficient algorithms to compute such a sparsifier assuming each $f_i$ can be evaluated efficiently.

Our results generalize the classic case of $\ell_p$ sparsification, where $f_i(z) = |z|^p$, for $p \in (0, 2]$, and give the first near-linear size sparsifiers in the well-studied setting of the Huber loss function and its generalizations, e.g., $f_i(z) = \min{|z|^p, |z|^2}$ for $0 < p \leq 2$. Our sparsification algorithm can be applied to give near-optimal reductions for optimizing a variety of generalized linear models including $\ell_p$ regression for $p \in (1, 2]$ to high accuracy, via solving $(\log n)^{O(1)}$ sparse regression instances with $m \le n(\log n)^{O(1)}$, plus runtime proportional to the number of nonzero entries in the vectors $a_1, \dots, a_m$.

For any norms $N_1,\ldots,N_m$ on $\mathbb{R}^n$ and $N(x) := N_1(x)+\cdots+N_m(x)$, we show there is a sparsified norm $\tilde{N}(x) = w_1 N_1(x) + \cdots + w_m N_m(x)$ such that $|N(x) - \tilde{N}(x)| \leq \epsilon N(x)$ for all $x \in \mathbb{R}^n$, where $w_1,\ldots,w_m$ are non-negative weights, of which only $O(\epsilon^{-2} n \log(n/\epsilon) (\log n)^{2.5} )$ are non-zero.

Additionally, we show that such weights can be found with high probability in time $O(m (\log n)^{O(1)} + \mathrm{poly}(n)) T$, where $T$ is the time required to evaluate a norm $N_i(x)$, assuming that $N(x)$ is $\mathrm{poly}(n)$-equivalent to the Euclidean norm. This immediately yields analogous statements for sparsifying sums of symmetric submodular functions. More generally, we show how to sparsify sums of $p$th powers of norms when the sum is $p$-uniformly smooth.

In a hypergraph on $n$ vertices where $D$ is the maximum size of a hyperedge, there is a weighted hypergraph spectral $\varepsilon$-sparsifier with at most $O(\varepsilon^{-2} \log(D) \cdot n \log n)$ hyperedges. This improves over the bound of Kapralov, Krauthgamer, Tardos and Yoshida (2021) who achieve $O(\varepsilon^{-4} n (\log n)^3)$, as well as the bound $O(\varepsilon^{-2} D^3 n \log n)$ obtained by Bansal, Svensson, and Trevisan (2019).

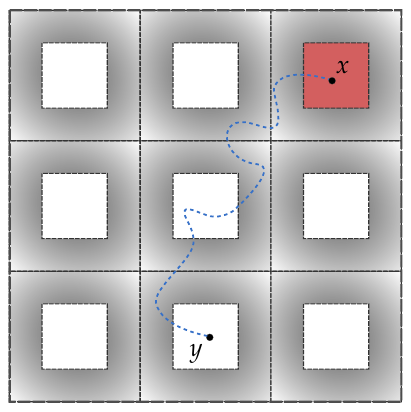
For reversible random networks, we exhibit a relationship between the almost sure spectral dimension and the Euclidean growth exponent, which is the smallest asymptotic rate of volume growth over all embeddings of the network into a Hilbert space. Using metric embedding theory, it is then shown that the Euclidean growth exponent coincides with the metric growth exponent. This simplifies and generalizes a powerful tool for bounding the spectral dimension in random networks.

We investigate the validity of the “Einstein relations” in the general setting of unimodular random networks. These are equalities relating scaling exponents:

where $d_w$ is the walk dimension, $d_f$ is the fractal dimension, $d_s$ is the spectral dimension, and $\tilde{\zeta}$ is the resistance exponent. Roughly speaking, this relates the mean displacement and return probability of a random walker to the density and conductivity of the underlying medium. We show that if $d_f$ and $\tilde{\zeta} \geq 0$ exist, then $d_w$ and $d_s$ exist, and the aforementioned equalities hold. Moreover, our primary new estimate $d_w \geq d_f + \tilde{\zeta}$ is established for all $\tilde{\zeta} \in \mathbb{R}$.

This has a number of consequences for unimodular random networks arising from statistical physics.

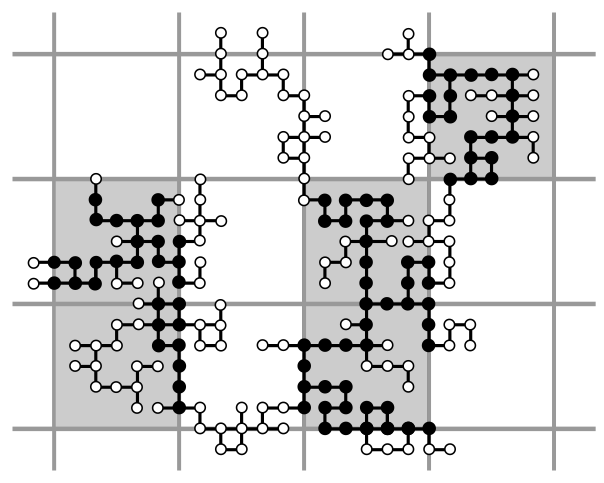
We show that random walk on the incipient infinite cluster (IIC) of two-dimensional critical percolation is subdiffusive in the chemical distance (i.e., in the intrinisc graph metric). Kesten (1986) famously showed that this is true for the Euclidean distance, but it is known that the chemical distance is typically asymptotically larger.

More generally, we show that subdiffusivity in the chemical distance holds for stationary random graphs of polynomial volume growth, as long as there is a multiscale way of covering the graph so that “deep patches” have “thin backbones.” Our estimates are quantitative and give explicit bounds in terms of the one and two-arm exponents.

Consider an infinite planar graph with uniform polynomial growth of degree $d > 2$. Many examples of such graphs exhibit similar geometric and spectral properties, and it has been conjectured that this is necessary. We present a family of counterexamples. In particular, we show that for every rational $d > 2$, there is a planar graph with uniform polynomial growth of degree $d$ on which the random walk is transient, disproving a conjecture of Benjamini (2011).

By a well-known theorem of Benjamini and Schramm, such a graph cannot be a unimodular random graph. We also give examples of unimodular random planar graphs of uniform polynomial growth with unexpected properties. For instance, graphs of (almost sure) uniform polynomial growth of every rational degree $d > 2$ for which the speed exponent of the walk is larger than $1/d$, and in which the complements of all balls are connected. This resolves negatively two questions of Benjamini and Papasoglou (2011).

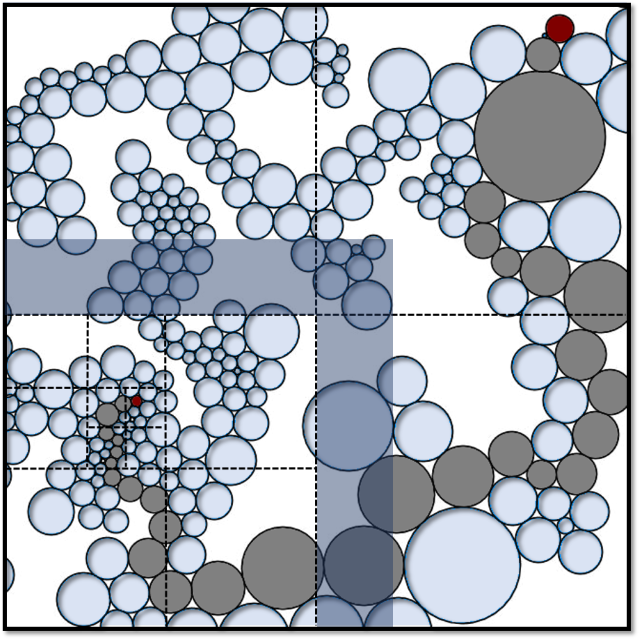
If \((G, \rho)\) is the distributional limit of finite graphs that can be sphere-packed in \(\mathbb{R}^d\), then the conformal growth exponent of \((G, \rho)\) is at most d. In other words, there exists a unimodular “unit volume” weighting of the graph metric on G such that the volume growth of balls is asymptotically polynomial with exponent d. This generalizes to graphs that can be quasisymmetrically packed in an Ahlfors d-regular metric measure space. Using our previous work, it gives bounds on the almost sure spectral dimension of G.

For a unimodular random graph \((G, \rho)\), we consider deformations of its intrinsic path metric by a (random) weighting of its vertices. This leads to the notion of the conformal growth exponent of \((G, \rho)\), which is the best asymptotic degree of volume growth of balls that can be achieved by such a weighting. Under moment conditions on the degree of the root, we show that the conformal growth exponent of a unimodular random graph bounds its almost sure spectral dimension.

For two-dimensional growth, one obtains more precise information about recurrence, the heat kernel, and subdiffusivity of the random walk. In particular, this gives a new method for studying the uniform infinite planar triangulation (UIPT) and quadrangulation (UIPQ).

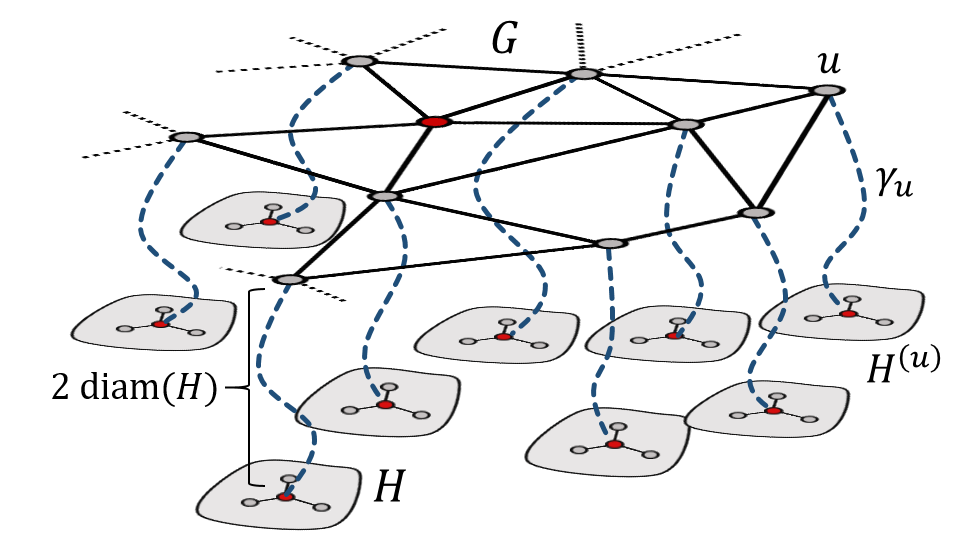
We show that if $(G,\rho)$ is a stationary random graph of annealed polynomial growth, then almost surely there is an infinite sequence of times at which the random walk started from x is at most diffusive. This result is new even in the case when G is a stationary random subgraph of $\mathbb{Z}^d$. Combined with the work of Benjamini, Duminil-Copin, Kozma, and Yadin, it implies that G almost surely does not admit a non-constant harmonic function of sublinear growth.

To complement this, we argue that passing to a subsequence of times is necessary, as there are stationary random graphs of (almost sure) polynomial growth where the random walk is almost surely superdiffisuve at an infinite subset of times.

Addendum: In the paper, we ask whether passing to a subsequence of times is necessary when $G$ is a stationary random subgraph of $\mathbb{Z}^d$. For the case $d=2$, it holds for all times using my paper with Ding and Peres. For $d$ sufficiently large, passing to a subsequence of times is necessary; this can be proved by showing that our stationary random graph occurs as a stationary random subgraph of $\mathbb{Z}^d_{\infty}$, using my paper with Krauthgamer.

We show that if the random walk on a graph has positive coarse Ricci curvature in the sense of Ollivier, then the stationary measure satisfies a \(W^1\) transport-entropy inequality. Peres and Tetali have conjectured a stronger consequence, that a modified log-Sobolev inequality (MLSI) should hold, in analogy with the setting of Markov diffusions. We discuss how our entropy interpolation approach suggests a natural attack on the MLSI conjecture.

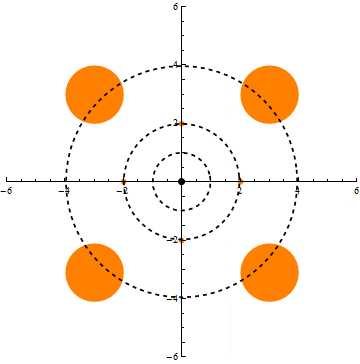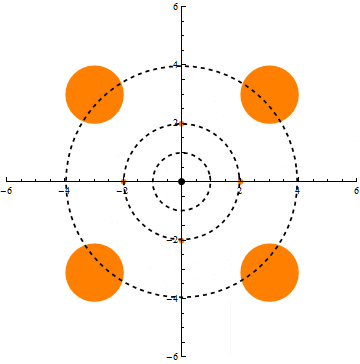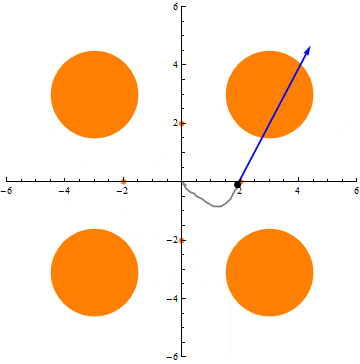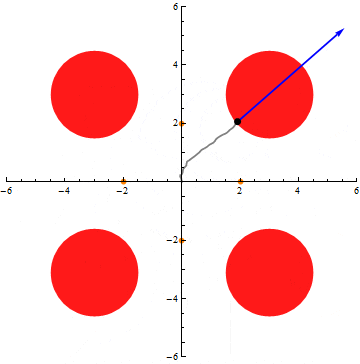
We show that under the Ornstein-Uhlenbeck semigroup (i.e., the natural diffusion process) on n-dimensional Gaussian space, any nonnegative, measurable function exhibits a uniform tail bound better than that implied by Markov’s inequality and conservation of mass. This confirms positively the Gaussian limiting case of Talagrand’s convolution conjecture (1989).

Video: Talagrand’s convolution conjecture and geometry via coupling (IAS)

Recall the classical hypothesis testing setting with two convex sets of probability distributions $P$ and $Q$. One receives either $n$ i.i.d. samples from a distribution $p \in P$ or from a distribution $q \in Q$ and wants to decide from which set the points were sampled. It is known that the optimal exponential rate at which errors decrease can be achieved by a simple maximum-likelihood ratio test which does not depend on $p$ or $q$, but only on the sets $P$ and $Q$. We consider an adaptive generalization of this model where the choice of $p \in P$ and $q \in Q$ can change in each sample in some way that depends arbitrarily on the previous samples. In other words, in the $k$th round, an adversary, having observed all the previous samples in rounds $1,…,k-1$, chooses $p_k \in P$ and $q_k \in Q$, with the goal of confusing the hypothesis test. We prove that even in this case, the optimal exponential error rate can be achieved by a simple maximum-likelihood test that depends only on $P$ and $Q$.

We then show that the adversarial model has applications in hypothesis testing for quantum states using restricted measurements. For example, it can be used to study the problem of distinguishing entangled states from the set of all separable states using only measurements that can be implemented with local operations and classical communication (LOCC). The basic idea is that in our setup, the deleterious effects of entanglement can be simulated by an adaptive classical adversary. We prove a quantum Stein’s Lemma in this setting: In many circumstances, the optimal hypothesis testing rate is equal to an appropriate notion of quantum relative entropy between two states. In particular, our arguments yield an alternate proof of Li and Winter’s recent strengthening of strong subadditivity for quantum relative entropy.

For two metric spaces $X$ and $Y$, say that $X$ threshold-embeds into $Y$ if there exist a number $K > 0$ and a family of Lipschitz maps $\{\varphi_{\tau} : X \to Y : \tau > 0 \}$ such that for every $x,y \in X$, \[d_X(x,y) \geq \tau \implies d_Y(\varphi_{\tau}(x),\varphi_{\tau}(y)) \geq \|\varphi_{\tau}\|_{\mathrm{Lip}} \frac{\tau}{K},\] where $\|\varphi_{\tau}\|_{\mathrm{Lip}}$ denotes the Lipschitz constant of $\varphi_{\tau}$.

We show that if a metric space $X$ threshold-embeds into a Hilbert space, then $X$ has Markov type 2. As a consequence, planar graph metrics and doubling metrics have Markov type 2, answering questions of Naor, Peres, Schramm, and Sheffield. More generally, if a metric space $X$ threshold-embeds into a $p$-uniformly smooth Banach space, then $X$ has Markov type $p$. Our results suggest some non-linear analogs of Kwapien’s theorem. For instance, a subset $X \subseteq L_1$ threshold-embeds into Hilbert space if and only if $X$ has Markov type 2.

We show that the cover time of a graph can be related to the square of the maximum of the associated Gaussian free field. This yields a positive answer to a question of Aldous and Fill (1994) on deterministic approximations to the cover time, and positively resolves the Blanket Time conjecture of Winkler and Zuckerman (1996).

Video: Cover times of graphs and the Gaussian free field (Newton Institute)
Notes: Majorizing measures and Gaussian processes
Related questions and conjectures (all solved except the one after Lemma 4)

See also the related preprint of Alex Zhai that resolves our main conjecture.

We prove diffusive lower bounds on the rate of escape of the random walk on infinite transitive graphs. Similar estimates hold for finite graphs, up to the relaxation time of the walk. Our approach uses nonconstant equivariant harmonic mappings taking values in a Hilbert space. For the special case of discrete, amenable groups, we present a more explicit proof of the Mok-Korevaar-Schoen theorem on the existence of such harmonic maps by constructing them from the heat flow on a Folner set.

We initiate a systematic study of eigenvectors of random graphs. Whereas much is known about eigenvalues of graphs and how they reflect properties of the underlying graph, relatively little is known about the corresponding eigenvectors. Our main focus in this paper is on the nodal domains associated with the different eigenfunctions. In the analogous realm of Laplacians of Riemannian manifolds, nodal domains have been the subject of intensive research for well over a hundred years. Graphical nodal domains turn out to have interesting and unexpected properties.

Our main theorem asserts that there is a constant c such that for almost every graph G, each eigenfunction of G has at most two large nodal domains, and in addition at most c exceptional vertices outside these primary domains. We also discuss variations of these questions and briefly report on some numerical experiments which, in particular, suggest that almost surely there are just two nodal domains and no exceptional vertices.

We show that an infinite weighted tree admits a bi-Lipschitz embedding into Hilbert space if and only if it does not contain arbitrarily large complete binary trees with uniformly bounded distortion. We also introduce a new metric invariant called Markov convexity, and show how it can be used to compute the Euclidean distortion of any metric tree up to universal factors.