Publications
[metric embeddings]
We consider the sparsification of sums \(F : \mathbb{R}^n \to \mathbb{R}_+\) where \(F(x) = f_1(\langle a_1,x\rangle) + \cdots + f_m(\langle a_m,x\rangle)\) for vectors $a_1,\ldots,a_m \in \mathbb{R}^n$ and functions $f_1,\ldots,f_m : \mathbb{R} \to \mathbb{R}_+$. We show that $(1+\varepsilon)$-approximate sparsifiers of $F$ with support size $\frac{n}{\varepsilon^2} (\log \frac{n}{\varepsilon})^{O(1)}$ exist whenever the functions $f_1,\ldots,f_m$ are symmetric, monotone, and satisfy natural growth bounds. Additionally, we give efficient algorithms to compute such a sparsifier assuming each $f_i$ can be evaluated efficiently.
Our results generalize the classic case of $\ell_p$ sparsification, where $f_i(z) = |z|^p$, for $p \in (0, 2]$, and give the first near-linear size sparsifiers in the well-studied setting of the Huber loss function and its generalizations, e.g., $f_i(z) = \min{|z|^p, |z|^2}$ for $0 < p \leq 2$. Our sparsification algorithm can be applied to give near-optimal reductions for optimizing a variety of generalized linear models including $\ell_p$ regression for $p \in (1, 2]$ to high accuracy, via solving $(\log n)^{O(1)}$ sparse regression instances with $m \le n(\log n)^{O(1)}$, plus runtime proportional to the number of nonzero entries in the vectors $a_1, \dots, a_m$.
For any norms $N_1,\ldots,N_m$ on $\mathbb{R}^n$ and $N(x) := N_1(x)+\cdots+N_m(x)$, we show there is a sparsified norm $\tilde{N}(x) = w_1 N_1(x) + \cdots + w_m N_m(x)$ such that $|N(x) - \tilde{N}(x)| \leq \epsilon N(x)$ for all $x \in \mathbb{R}^n$, where $w_1,\ldots,w_m$ are non-negative weights, of which only $O(\epsilon^{-2} n \log(n/\epsilon) (\log n)^{2.5} )$ are non-zero.
Additionally, we show that such weights can be found with high probability in time $O(m (\log n)^{O(1)} + \mathrm{poly}(n)) T$, where $T$ is the time required to evaluate a norm $N_i(x)$, assuming that $N(x)$ is $\mathrm{poly}(n)$-equivalent to the Euclidean norm. This immediately yields analogous statements for sparsifying sums of symmetric submodular functions. More generally, we show how to sparsify sums of $p$th powers of norms when the sum is $p$-uniformly smooth.
@inproceedings{JLLS23,
AUTHOR = {Arun Jambulapati and James R. Lee and Yang P. Liu and Aaron
Sidford},
BIBSOURCE = {dblp computer science bibliography, https://dblp.org},
BIBURL = {https://dblp.org/rec/conf/focs/JambulapatiLLS23.bib},
BOOKTITLE = {64th {IEEE} Annual Symposium on Foundations of Computer Science,
{FOCS} 2023, Santa Cruz, CA, USA, November 6-9,
2023},
DOI = {10.1109/FOCS57990.2023.00119},
PAGES = {1953--1962},
PUBLISHER = {{IEEE}},
TIMESTAMP = {Tue, 02 Jan 2024 15:09:54 +0100},
TITLE = {Sparsifying Sums of Norms},
URL = {https://doi.org/10.1109/FOCS57990.2023.00119},
YEAR = {2023}
}
For reversible random networks, we exhibit a relationship between the almost sure spectral dimension and the Euclidean growth exponent, which is the smallest asymptotic rate of volume growth over all embeddings of the network into a Hilbert space. Using metric embedding theory, it is then shown that the Euclidean growth exponent coincides with the metric growth exponent. This simplifies and generalizes a powerful tool for bounding the spectral dimension in random networks.
@article{Lee23ijm,
AUTHOR = {Lee, James R.},
DOI = {10.1007/s11856-023-2520-x},
FJOURNAL = {Israel Journal of Mathematics},
ISSN = {0021-2172,1565-8511},
JOURNAL = {Israel J. Math.},
NUMBER = {2},
PAGES = {417--439},
TITLE = {Spectral dimension, {E}uclidean embeddings, and the metric growth
exponent},
URL = {https://doi.org/10.1007/s11856-023-2520-x},
VOLUME = {256},
YEAR = {2023}
}
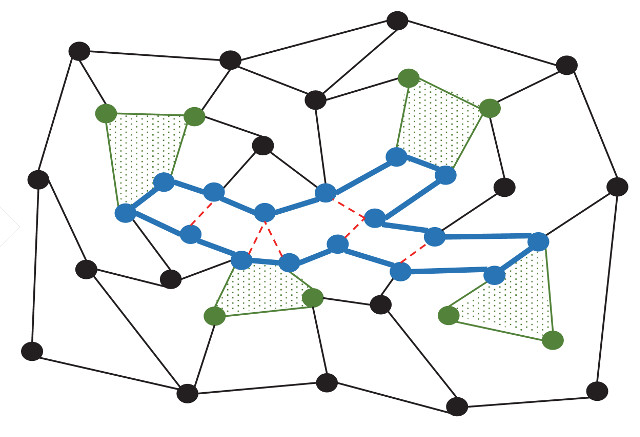
We establish new and improved bounds on the flow-cut gap in planar flow networks where the terminals lie on a small number of faces. The classical Okamura-Seymour theorem (1981) shows that when all terminals lie on a single face, the flow-cut gap is exactly 1. We show that if the terminals lie on $\gamma$ faces, the flow-cut gap is $O(\log \gamma)$. This is proved by embedding the terminal metric into a distribution over trees with distortion $O(\log \gamma)$, which is tight up to the implied constant factor.
@inproceedings{KLR19,
AUTHOR = {Krauthgamer, Robert and Lee, James R. and Rika, Havana},
BOOKTITLE = {Proceedings of the {T}hirtieth {A}nnual {ACM}-{SIAM} {S}ymposium on
{D}iscrete {A}lgorithms},
PAGES = {525--534},
PUBLISHER = {SIAM, Philadelphia, PA},
TITLE = {Flow-cut gaps and face covers in planar graphs},
YEAR = {2019}
}
We give a poly(log k)-competitive randomized algorithm for the k-server problem on general metric spaces. The best previous result independent of the underlying metric space is the 2k-1 competitive ratio established for the deterministic work function algorithm by Koutsoupias and Papadimitriou (1995).
Since deterministic algorithms can do no better than k on any metric space with at least k+1 points, this establishes that for every metric space on which the problem is non-trivial, randomized algorithms give an exponential improvement over deterministic algorithms. The approach employs our previous algorithm for the fractional k-server problem on HSTs.
[This paper has been withdrawn]@incollection{LeeFOCS18,
AUTHOR = {Lee, James R.},
BOOKTITLE = {59th {A}nnual {IEEE} {S}ymposium on {F}oundations of {C}omputer
{S}cience---{FOCS} 2018},
PAGES = {438--449},
PUBLISHER = {IEEE Computer Soc., Los Alamitos, CA},
TITLE = {Fusible {HST}s and the randomized {$k$}-server conjecture},
YEAR = {2018}
}
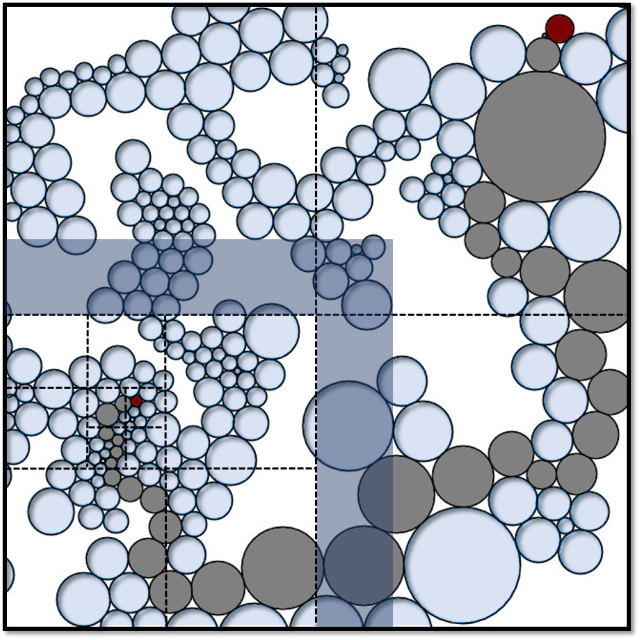
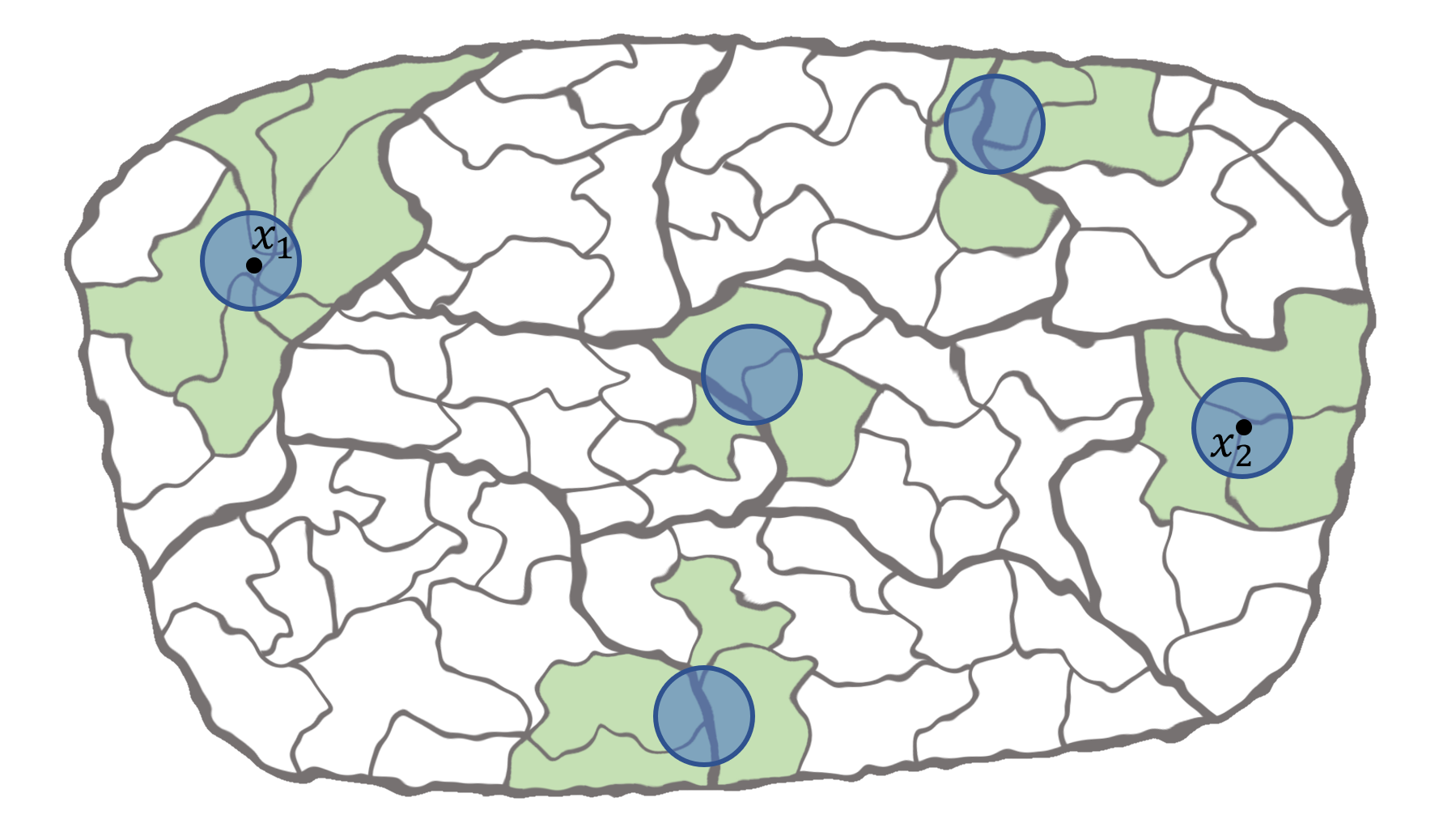
If \((G, \rho)\) is the distributional limit of finite graphs that can be sphere-packed in \(\mathbb{R}^d\), then the conformal growth exponent of \((G, \rho)\) is at most d. In other words, there exists a unimodular “unit volume” weighting of the graph metric on G such that the volume growth of balls is asymptotically polynomial with exponent d. This generalizes to graphs that can be quasisymmetrically packed in an Ahlfors d-regular metric measure space. Using our previous work, it gives bounds on the almost sure spectral dimension of G.
@article{LeeGAFA18,
AUTHOR = {Lee, James R.},
FJOURNAL = {Geometric and Functional Analysis},
JOURNAL = {Geom. Funct. Anal.},
NUMBER = {4},
PAGES = {1091--1130},
TITLE = {Discrete uniformizing metrics on distributional limits of sphere
packings},
VOLUME = {28},
YEAR = {2018}
}
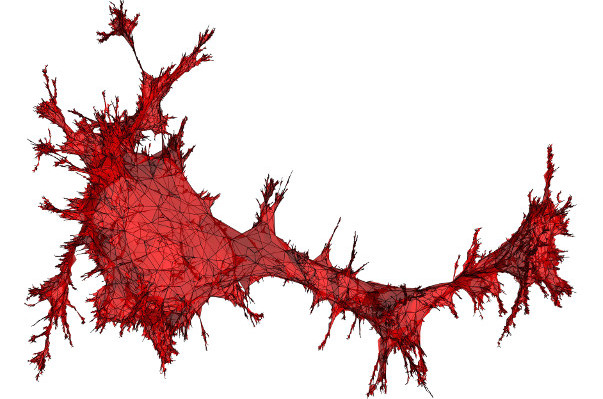
[credit: Jérémie Bettinelli]
For a unimodular random graph \((G, \rho)\), we consider deformations of its intrinsic path metric by a (random) weighting of its vertices. This leads to the notion of the conformal growth exponent of \((G, \rho)\), which is the best asymptotic degree of volume growth of balls that can be achieved by such a weighting. Under moment conditions on the degree of the root, we show that the conformal growth exponent of a unimodular random graph bounds its almost sure spectral dimension.
For two-dimensional growth, one obtains more precise information about recurrence, the heat kernel, and subdiffusivity of the random walk. In particular, this gives a new method for studying the uniform infinite planar triangulation (UIPT) and quadrangulation (UIPQ).
@article{LeeAOP21,
AUTHOR = {James R. Lee},
DOI = {10.1214/20-AOP1480},
FJOURNAL = {Annals of Probability},
ISSN = {0091-1798},
JOURNAL = {Ann. Probab.},
NUMBER = {6},
PAGES = {2671-2731},
TITLE = {Conformal growth rates and spectral geometry on distributional
limits of graphs},
VOLUME = {49},
YEAR = {2021}
}
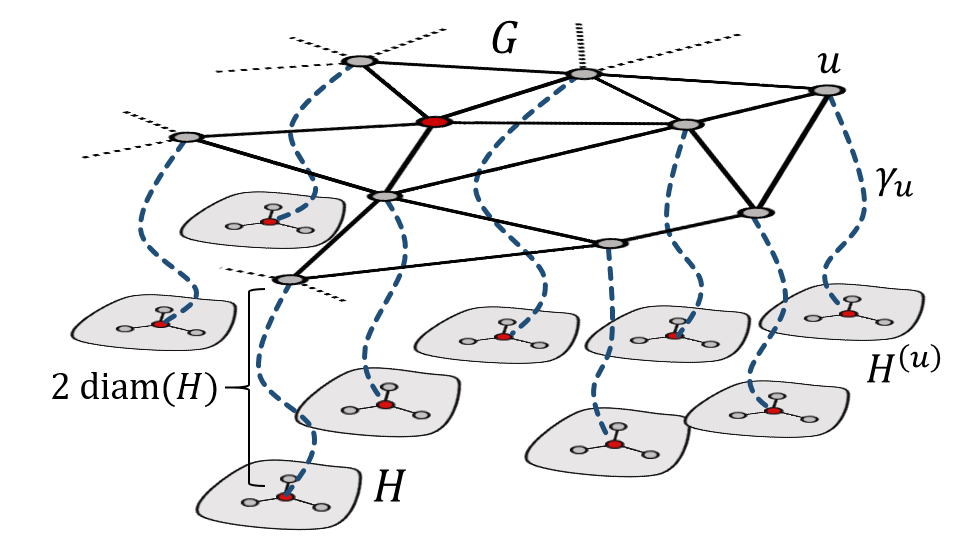
We show that if $(G,\rho)$ is a stationary random graph of annealed polynomial growth, then almost surely there is an infinite sequence of times at which the random walk started from x is at most diffusive. This result is new even in the case when G is a stationary random subgraph of $\mathbb{Z}^d$. Combined with the work of Benjamini, Duminil-Copin, Kozma, and Yadin, it implies that G almost surely does not admit a non-constant harmonic function of sublinear growth.
To complement this, we argue that passing to a subsequence of times is necessary, as there are stationary random graphs of (almost sure) polynomial growth where the random walk is almost surely superdiffisuve at an infinite subset of times.
Addendum: In the paper, we ask whether passing to a subsequence of times is necessary when $G$ is a stationary random subgraph of $\mathbb{Z}^d$. For the case $d=2$, it holds for all times using my paper with Ding and Peres. For $d$ sufficiently large, passing to a subsequence of times is necessary; this can be proved by showing that our stationary random graph occurs as a stationary random subgraph of $\mathbb{Z}^d_{\infty}$, using my paper with Krauthgamer.
@article {GLP17,
AUTHOR = {Ganguly, Shirshendu and Lee, James R. and Peres, Yuval},
TITLE = {Diffusive estimates for random walks on stationary random
graphs of polynomial growth},
JOURNAL = {Geom. Funct. Anal.},
FJOURNAL = {Geometric and Functional Analysis},
VOLUME = {27},
YEAR = {2017},
NUMBER = {3},
PAGES = {596--630},
}

A region intersection graph over a base graph \(G_0\) is a graph \(G\) whose vertices correspond to connected subsets of \(G_0\) with an edge between two vertices if the corresponding regions intersect. We show that if \(G_0\) excludes the complete graph \(K_h\) as a minor, then every region intersection graph over \(G_0\) with m edges has a balanced separator with \(O(\sqrt{m})\) nodes. If \(G\) has uniformly bounded vertex degrees, we show the separator is found by spectral partitioning.
A string graph is the intersection graph of continuous arcs in the plane. The preceding result implies that every string graph with m edges has a balanced separator of size \(O(\sqrt{m})\). This bound is optimal, as it generalizes the planar separator theorem. It confirms a conjecture of Fox and Pach (2010) and improves over the \(O(\sqrt{m} \log m)\) bound of Matousek (2013).
@inproceedings{LeeStrings17,
author = {James R. Lee},
title = {Separators in Region Intersection Graphs},
booktitle = {8th Innovations in Theoretical Computer Science Conference, {ITCS}
2017, January 9-11, 2017, Berkeley, CA, {USA}},
pages = {1:1--1:8},
year = {2017},
}
There is a constant c > 0 such that for every $\varepsilon \in (0,1)$ and $n \geq 1/\varepsilon^2$, the following holds. Any mapping from the $n$-point star metric into $\ell_1^d$ with bi-Lipschitz distortion $1+\varepsilon$ requires dimension \[d \geq \frac{c \log n}{\varepsilon^2 \log (1/\varepsilon)}.\]
The classical Okamura-Seymour theorem states that for an edge-capacitated, multi-commodity flow instance in which all terminals lie on a single face of a planar graph, there exists a feasible concurrent flow if and only if the cut conditions are satisfied. Simple examples show that a similar theorem is impossible in the node-capacitated setting. Nevertheless, we prove that an approximate flow/cut theorem does hold: For some universal c > 0, if the node cut conditions are satisfied, then one can simultaneously route a c-fraction of all the demands.
This answers an open question of Chekuri and Kawarabayashi. More generally, we show that this holds in the setting of multi-commodity polymatroid networks introduced by Chekuri, et. al. Our approach employs a new type of random metric embedding in order to round the convex programs corresponding to these more general flow problems.
@article {LMM15,
AUTHOR = {Lee, James R. and Mendel, Manor and Moharrami, Mohammad},
TITLE = {A node-capacitated {O}kamura-{S}eymour theorem},
JOURNAL = {Math. Program.},
FJOURNAL = {Mathematical Programming},
VOLUME = {153},
YEAR = {2015},
NUMBER = {2, Ser. A},
PAGES = {381--415},
}
For two metric spaces $X$ and $Y$, say that $X$ threshold-embeds into $Y$ if there exist a number $K > 0$ and a family of Lipschitz maps $\{\varphi_{\tau} : X \to Y : \tau > 0 \}$ such that for every $x,y \in X$, \[d_X(x,y) \geq \tau \implies d_Y(\varphi_{\tau}(x),\varphi_{\tau}(y)) \geq \|\varphi_{\tau}\|_{\mathrm{Lip}} \frac{\tau}{K},\] where $\|\varphi_{\tau}\|_{\mathrm{Lip}}$ denotes the Lipschitz constant of $\varphi_{\tau}$.
We show that if a metric space $X$ threshold-embeds into a Hilbert space, then $X$ has Markov type 2. As a consequence, planar graph metrics and doubling metrics have Markov type 2, answering questions of Naor, Peres, Schramm, and Sheffield. More generally, if a metric space $X$ threshold-embeds into a $p$-uniformly smooth Banach space, then $X$ has Markov type $p$. Our results suggest some non-linear analogs of Kwapien’s theorem. For instance, a subset $X \subseteq L_1$ threshold-embeds into Hilbert space if and only if $X$ has Markov type 2.
@article {DLP13,
AUTHOR = {Ding, Jian and Lee, James R. and Peres, Yuval},
TITLE = {Markov type and threshold embeddings},
JOURNAL = {Geom. Funct. Anal.},
FJOURNAL = {Geometric and Functional Analysis},
VOLUME = {23},
YEAR = {2013},
NUMBER = {4},
PAGES = {1207--1229},
}
The $2$-sum embedding conjecture (Lee-Sidiropoulos, FOCS 2009) states that all the shortest-path metrics supported on a family of graphs $\mathcal F$ admit a uniformly bi-Lipschitz embedding into $L_1$ if and only if the same property holds for the closure of $\mathcal F$ under edge sums. The problem has an equivalent formulation in terms of multi-commodity flow/cut gaps and appears to be a fundamental step in resolving the well-studied question of which families of graphs admit an approximate multi-commodity max-flow/min-cut theorem.
The $2$-sum conjecture is known to be true when $\mathcal F = {K_3}$, where $K_n$ denotes the complete graph on $n$ vertices; this is equivalent to the seminal result of Gupta, Newman, Rabinovich, and Sinclair (Combinatorica, 2004) on embeddings of series-parallel graphs into $L_1$. For $\mathcal F = {K_4}$, the conjecture was confirmed by Chakrabarti, Jaffe, Lee, and Vincent (FOCS 2008). In the present paper, we prove the conjecture holds for any finite family of graphs $\mathcal F$. In fact, we obtain a quantitatively optimal result: Any path metric on a graph formed by $2$-sums of arbitrarily many copies of $K_n$ embeds into $L_1$ with distortion $O(\log n)$. This is a consequence of a more general theorem that characterizes the $L_1$ distortion of the 2-sum closure of any family $\mathcal F$ in terms of constrained embeddings of the members of $\mathcal F$.
@inproceedings{LeePoore13,
author = {James R. Lee and
Daniel E. Poore},
title = {On the 2-sum embedding conjecture},
booktitle = {Symposuim on Computational Geometry 2013, SoCG '13, Rio de Janeiro,
Brazil, June 17-20, 2013},
pages = {197--206},
year = {2013},
}
For every \(\varepsilon > 0\), any subset of \(\mathbb{R}^n\) with Hausdorff dimension larger than \((1-\varepsilon) n\) must have ultrametric distortion larger than \(1/(4\varepsilon)\).
@article {LMM12,
AUTHOR = {Lee, James R. and Mendel, Manor and Moharrami, Mohammad},
TITLE = {On the {H}ausdorff dimension of ultrametric subsets in {$\Bbb
R^n$}},
JOURNAL = {Fund. Math.},
FJOURNAL = {Fundamenta Mathematicae},
VOLUME = {218},
YEAR = {2012},
NUMBER = {3},
PAGES = {285--290},
}

A basic fact in spectral graph theory is that the number of connected components in an undirected graph is equal to the multiplicity of the eigenvalue zero in the Laplacian matrix of the graph. In particular, the graph is disconnected if and only if there are at least two eigenvalues equal to zero. Cheeger’s inequality and its variants provide a robust version of the latter fact; they state that a graph has a sparse cut if and only if there are at least two eigenvalues that are close to zero.
It has been conjectured that an analogous characterization holds for higher multiplicities: There are k eigenvalues close to zero if and only if the vertex set can be partitioned into k subsets, each defining a sparse cut. We resolve this conjecture positively. Our result provides a theoretical justification for clustering algorithms that use the bottom k eigenvectors to embed the vertices into \(\mathbb{R}^k\), and then apply geometric considerations to the embedding. We also show that these techniques yield a nearly optimal quantitative connection between the expansion of sets of measure ≈ 1/k and the kth smallest eigenvalue of the normalized Laplacian.
Notes: A no frills proof of the higher-order Cheeger inequality
Related: One hundred hours of lectures from the SGT program at the Simons Institute.
Related: Laurent Miclo uses the higher-order Cheeger inequality for the basis of his resolution of Hoegh-Krohn and Simon’s conjecture that every hyperbounded operator has a spectral gap.
@article{LOT14,
AUTHOR = {Lee, James R. and Gharan, Shayan Oveis and Trevisan, Luca},
FJOURNAL = {Journal of the ACM},
JOURNAL = {J. ACM},
NUMBER = {6},
PAGES = {Art. 37, 30},
TITLE = {Multiway spectral partitioning and higher-order {C}heeger
inequalities},
VOLUME = {61},
YEAR = {2014}
}
We show that every $n$-point tree metric admits a $(1+\varepsilon)$-bi-Lipschitz embedding into a $C(\varepsilon) \log n$-dimensional $\ell_1$ space for every $\varepsilon > 0$, where $C(\varepsilon) \leq O((1/\varepsilon)^4 \log (1/\varepsilon))$. This matches the natural volume lower bound up to a factor depending only on $\varepsilon$. Previously this was unknown even for complete binary trees.
@article {LLM13,
AUTHOR = {Lee, James R. and de Mesmay, Arnaud and Moharrami, Mohammad},
TITLE = {Dimension reduction for finite trees in {$\ell_1$}},
JOURNAL = {Discrete Comput. Geom.},
FJOURNAL = {Discrete \& Computational Geometry. An International Journal
of Mathematics and Computer Science},
VOLUME = {50},
YEAR = {2013},
NUMBER = {4},
PAGES = {977--1032},
}
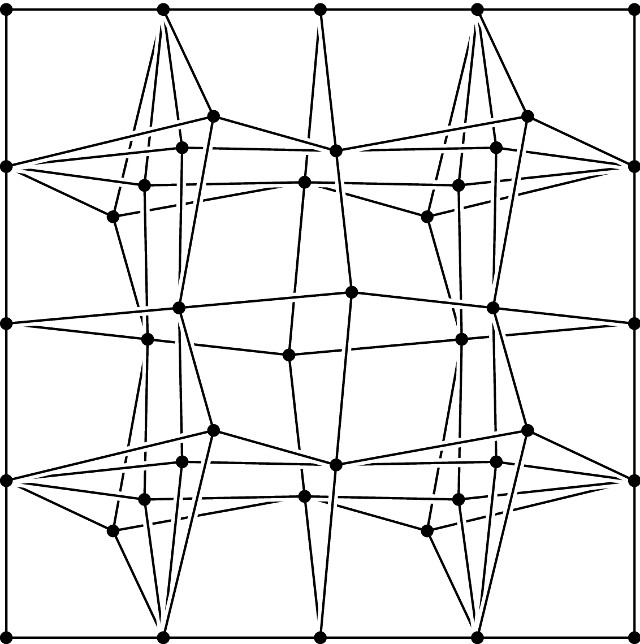
We show that there is a family of $n$-point uniformly doubling metrics that require bilipschitz distortion $\Omega\left(\sqrt{\frac{\log n}{\log \log n}}\right)$ under any embedding into $L_1$, matching the known upper bound to within an $O(\sqrt{\log \log n})$ factor.
@inproceedings{DBLP:conf/stoc/LeeS11,
author = {James R. Lee and
Anastasios Sidiropoulos},
title = {Near-optimal distortion bounds for embedding doubling spaces into
L\({}_{\mbox{1}}\)},
booktitle = {Proceedings of the 43rd {ACM} Symposium on Theory of Computing, {STOC}
2011, San Jose, CA, USA, 6-8 June 2011},
pages = {765--772},
year = {2011},
}
We show there exists a metric space $(X,d)$ such that $(X,\sqrt{d})$ admits a bilipschitz embedding into $L_2$, but $(X,d)$ does not admit an equivalent metric of negative type. In fact, we exhibit a strong quantitative bound: There are $n$-point subsets $Y_n \subseteq X$ such that any mapping of $(Y_n,d)$ to a metric of negative type incurs distortion at least $\tilde{\Omega}(\log n)^{1/4}$.
This answers an open question about the strength of strong vs. weak triangle inequalities in a number of semidefinite programs. Our construction sheds light on the power of various notions of “dual flows” that arise in algorithms for approximating the Sparsest Cut problem. It also has other interesting implications for bilipschitz embeddings of finite metric spaces.
@inproceedings{LMstoc10,
author = {James R. Lee and
Mohammad Moharrami},
editor = {Leonard J. Schulman},
title = {Bilipschitz snowflakes and metrics of negative type},
booktitle = {Proceedings of the 42nd {ACM} Symposium on Theory of Computing, {STOC}
2010, Cambridge, Massachusetts, USA, 5-8 June 2010},
pages = {621--630},
publisher = {{ACM}},
year = {2010},
}
We show that every graph of pathwidth $k$ embeds into a distribution over random trees with distortion $c(k)$. In particular, this implies that whenever a non-trivial minor-closed family $\mathcal{F}$ of graphs does not contain all trees, the multi-commodity max-flow/min-cut gap is uniformly bounded for all instances over $\mathcal{F}$.
@article{LS13,
AUTHOR = {Lee, James R. and Sidiropoulos, Anastasios},
FJOURNAL = {Combinatorica. An International Journal on Combinatorics and the
Theory of Computing},
JOURNAL = {Combinatorica},
NUMBER = {3},
PAGES = {349--374},
TITLE = {Pathwidth, trees, and random embeddings},
VOLUME = {33},
YEAR = {2013}
}
We show that for every $\alpha > 0$, there is an $n$-point metric space $(X,d)$ where every “scale” admits a Euclidean embedding with distortion at most $\alpha$, but any bi-Lipschitz embedding requires distortion $\Omega(\sqrt{\alpha \log n})$.
The matching upper bound was known to be tight at both endpoints (when $\alpha \asymp 1$ and $\alpha \asymp \log n$, but nowhere in between). This also shows that the “measured descent” method has an optimal asymptotic dependence on the parameters.
@article {JLM11,
AUTHOR = {Jaffe, Alexander and Lee, James R. and Moharrami, Mohammad},
TITLE = {On the optimality of gluing over scales},
JOURNAL = {Discrete Comput. Geom.},
FJOURNAL = {Discrete \& Computational Geometry. An International Journal
of Mathematics and Computer Science},
VOLUME = {46},
YEAR = {2011},
NUMBER = {2},
PAGES = {270--282},
}
We study the quantitative geometry of graphs in terms of their genus, using the structure of certain cut graphs. These are subgraphs whose removal leaves a planar graph.
@inproceedings{DBLP:conf/soda/LeeS10,
author = {James R. Lee and
Anastasios Sidiropoulos},
title = {Genus and the Geometry of the Cut Graph},
booktitle = {Proceedings of the Twenty-First Annual {ACM-SIAM} Symposium on Discrete
Algorithms, {SODA} 2010, Austin, Texas, USA, January 17-19, 2010},
pages = {193--201},
year = {2010},
}
Indyk and Sidiropoulos (2007) proved that any orientable graph of genus $g$ can be probabilistically embedded into a graph of genus $g−1$ with constant distortion. Viewing a graph of genus $g$ as embedded on the surface of a sphere with $g$ handles attached, Indyk and Sidiropoulos’ method gives an embedding into a distribution over planar graphs with distortion $O(g)$ by iteratively removing the handles. By removing all g handles at once, we present a probabilistic embedding with distortion $O(g^2)$ for both orientable and non-orientable graphs. Our result is obtained by showing that the nimum-cut graph of Erickson and Har Peled (2004) has low dilation, and then randomly cutting this graph out of the surface using the Peeling Lemma of Lee and Sidiropoulos (2009).
@article{BLS10,
AUTHOR = {Borradaile, Glencora and Lee, James R. and Sidiropoulos,
Anastasios},
FJOURNAL = {Computational Geometry. Theory and Applications},
JOURNAL = {Comput. Geom.},
NUMBER = {8},
PAGES = {655--662},
TITLE = {Randomly removing {$g$} handles at once},
VOLUME = {43},
YEAR = {2010}
}
We present a method for proving upper bounds on the eigenvalues of the graph Laplacian. A main step involves choosing an appropriate “Riemannian” metric to uniformize the geometry of the graph. In many interesting cases, the existence of such a metric is shown by examining the combinatorics of special types of flows. This involves proving new inequalities on the crossing number of graphs.
We use our method to show that for any positive integer k, the kth smallest eigenvalue of the Laplacian on an n-vertex, bounded-degree planar graph is O(k/n). This bound is asymptotically tight for every k, as it is easily seen to be achieved for square planar grids. We also extend this spectral result to graphs with bounded genus, and graphs which forbid fixed minors. Previously, such spectral upper bounds were only known for the case k=2.
@article {KLPT11,
AUTHOR = {Kelner, Jonathan A. and Lee, James R. and Price, Gregory N.
and Teng, Shang-Hua},
TITLE = {Metric uniformization and spectral bounds for graphs},
JOURNAL = {Geom. Funct. Anal.},
FJOURNAL = {Geometric and Functional Analysis},
VOLUME = {21},
YEAR = {2011},
NUMBER = {5},
PAGES = {1117--1143},
}
A method is presented for establishing an upper bound on the first non-trivial eigenvalue of the Laplacian of a finite graph. Our approach uses multi-commodity flows to deform the geometry of the graph, and the resulting metric is embedded into Euclidean space to recover a bound on the Rayleigh quotient.
Using this, we resolve positively a question of Spielman and Teng by proving that \(\lambda_2(G) \leq O(d h^6 \log h/n)\) whenever \(G\) is a \(K_h\)-minor-free graph with maximum degree \(d\). While the standard “sweep” algorithm applied to the second eigenvector of a graph my fail to find a good quotient cut in graphs of unbounded degree, the arguments here produce a vector that works for arbitrary graphs. This yields an alterante proof of the Alon-Seymour-Thomas theorem that every excluded-minor family of graphs has \(O(\sqrt{n})\)-node balanced separators.
Related: These methods are extended to higher eigenvalues in a
joint work with Kelner, Price, and Teng.
Related: These method form the basis for the uniformization and heat kernel bounds in Conformal
growth rates and spectral geometry on distributional limits of graphs.
@article {MR2665882,
AUTHOR = {Biswal, Punyashloka and Lee, James R. and Rao, Satish},
TITLE = {Eigenvalue bounds, spectral partitioning, and metrical
deformations via flows},
JOURNAL = {J. ACM},
FJOURNAL = {Journal of the ACM},
VOLUME = {57},
YEAR = {2010},
NUMBER = {3},
PAGES = {Art. 13, 23},
}
We establish that the multi-commodity max-flow/min-cut gap for series-parallel graphs is at least $2$. Our approach uses the coarse differentiation methodology of Eskin, Fisher, and Whyte.
@article {LR10,
AUTHOR = {Lee, James R. and Raghavendra, Prasad},
TITLE = {Coarse differentiation and multi-flows in planar graphs},
JOURNAL = {Discrete Comput. Geom.},
FJOURNAL = {Discrete \& Computational Geometry. An International Journal
of Mathematics and Computer Science},
VOLUME = {43},
YEAR = {2010},
NUMBER = {2},
PAGES = {346--362},
}
We give an explicit construction of subspaces $X \subseteq \mathbb{R}^N$ of dimension $(1-o(1)) N$ such that for every $x \in X$,
Through known connections between such Euclidean sections of $\ell_1$ and compressed sensing matrices, our result also gives explicit compressed sensing matrices for low compression factors for which basis pursuit is guaranteed to recover sparse signals. Our construction makes use of unbalanced bipartite graphs to impose local linear constraints on vectors in the subspace, and our analysis relies on expansion properties of the graph. This is inspired by similar constructions of error-correcting codes.
@article {GLR10,
AUTHOR = {Guruswami, Venkatesan and Lee, James R. and Razborov,
Alexander},
TITLE = {Almost {E}uclidean subspaces of {$\ell^N_1$} via expander
codes},
JOURNAL = {Combinatorica},
FJOURNAL = {Combinatorica. An International Journal on Combinatorics and
the Theory of Computing},
VOLUME = {30},
YEAR = {2010},
NUMBER = {1},
PAGES = {47--68},
}
We show that an infinite weighted tree admits a bi-Lipschitz embedding into Hilbert space if and only if it does not contain arbitrarily large complete binary trees with uniformly bounded distortion. We also introduce a new metric invariant called Markov convexity, and show how it can be used to compute the Euclidean distortion of any metric tree up to universal factors.
@article{LNP09,
AUTHOR = {Lee, James R. and Naor, Assaf and Peres, Yuval},
FJOURNAL = {Geometric and Functional Analysis},
JOURNAL = {Geom. Funct. Anal.},
NUMBER = {5},
PAGES = {1609--1659},
TITLE = {Trees and {M}arkov convexity},
VOLUME = {18},
YEAR = {2009}
}
We consider questions about vertex cuts in graphs, random walks in metric spaces, and dimension reduction in $\ell_1$ and $\ell_2$; these topics are intimately connected because they can each be reduced to the existence of various families of real-valued Lipschitz maps on certain metric spaces. We view these issues through the lens of shortest-path metrics on series-parallel graphs, and we discuss the implications for a variety of well-known open problems.
@inproceedings{DBLP:conf/stoc/BrinkmanKL07,
AUTHOR = {Bo Brinkman and Adriana Karagiozova and James R. Lee},
BOOKTITLE = {Proceedings of the 39th Annual {ACM} Symposium on Theory of
Computing, San Diego, California, USA, June 11-13,
2007},
DOI = {10.1145/1250790.1250882},
PAGES = {621--630},
TITLE = {Vertex cuts, random walks, and dimension reduction in series-
parallel graphs},
YEAR = {2007}
}
It is well-known that $\mathbb{R}^N$ has has subspaces of dimension proportional to $N$ on which the $\ell_1$ and $\ell_2$ norms are uniformly equivalent, but it is unknown how to construct them explicitly. We show that, for any $\delta > 0$, such a subspace can be generated using only $N^{\delta}$ random bits. This improves over previous constructions of Artstein-Avidan and Milman, and of Lovett and Sodin, which require $O(N log N)$, and $O(N)$ random bits, respectively.
It is known that such subspaces give rise to error-correcting codes over the reals and compressed sensing matrices. As in the work of Guruswami, Lee, and Razborov, our construction is the continuous analog of a Tanner code, and makes use of expander graphs to impose a collection of local linear constraints on vectors in the subspace. Our analysis is able to achieve uniform equivalence of the $\ell_1$ and $\ell_2$ norms (independent of the dimension). It has parallels to iterative decoding of Tanner codes, and leads to an analogous near-linear time algorithm for error-correction over reals.
@inproceedings{DBLP:conf/approx/GuruswamiLW08,
author = {Venkatesan Guruswami and
James R. Lee and
Avi Wigderson},
title = {Euclidean Sections of with Sublinear Randomness and Error-Correction
over the Reals},
booktitle = {Approximation, Randomization and Combinatorial Optimization. Algorithms
and Techniques, 11th International Workshop, {APPROX} 2008, and 12th
International Workshop, {RANDOM} 2008, Boston, MA, USA, August 25-27,
2008. Proceedings},
pages = {444--454},
year = {2008},
}
[credit: Patrick Massot]
We prove that the function \(d : \mathbb{R}^3 \times \mathbb{R}^3 \to [0,\infty)\) given by
is a metric on \(\mathbb{R}^3\) such that \((\mathbb{R}^3, \sqrt{d})\) is isometric to a subset of Hilbert space, yet \((\mathbb{R}^3,d)\) does not admit a bi-Lipschitz embedding into \(L_1\). This yields a new simple counter example to the Goemans-Linial conjecture on the integrality gap of the SDP relaxation of the Sparsest Cut problem.
Our methods involve Fourier analytic techniques, combined with a breakthrough of Cheeger and Kleiner, along with classical results of Pansu on the differentiability of Lispchitz functions on the Heisenberg group.
@inproceedings{LN06,
author = {James R. Lee and
Assaf Naor},
title = {Lp metrics on the Heisenberg group and the Goemans-Linial conjecture},
booktitle = {47th Annual {IEEE} Symposium on Foundations of Computer Science {(FOCS}
2006), 21-24 October 2006, Berkeley, California, USA, Proceedings},
pages = {99--108},
year = {2006},
}
We present an $O(\sqrt{\log n} \log \log n)$ upper bound on the $(n-1)$-dimensional volume distortion of $n$-point subsets of a Euclidean space, nearly resolving the main open questions of [Dunagan-Vempala 2001] and [Krauthgamer-Linial-Magen 2004]. The best previous bound was $O(\log n)$ and our bound is nearly tight, as even the $2$-dimensional volume distortion of an $n$-vertex path is $\Omega(\sqrt{\log n})$.
@article{LeeVolume09,
AUTHOR = {Lee, James R.},
FJOURNAL = {Discrete \& Computational Geometry. An International Journal of
Mathematics and Computer Science},
JOURNAL = {Discrete Comput. Geom.},
NUMBER = {4},
PAGES = {590--615},
TITLE = {Volume distortion for subsets of {E}uclidean spaces},
VOLUME = {41},
YEAR = {2009}
}
We explore approximation algorithms on negatively curved metric spaces in the sense of Gromov. For instance, we show that the Traveling Salesman Problem admits a PTAS when the set of points lies in hyperbolic $d$-space.
@inproceedings{KL06,
author = {Robert Krauthgamer and
James R. Lee},
title = {Algorithms on negatively curved spaces},
booktitle = {47th Annual {IEEE} Symposium on Foundations of Computer Science {(FOCS}
2006), 21-24 October 2006, Berkeley, California, USA, Proceedings},
pages = {119--132},
year = {2006},
}
We observe that combining the techniques behind the Sparsest Cut SDP analysis of Arora, Rao, and Vazirani, with the rounding algorithm of Rao and Richa yields an $O(\sqrt{\log n} \log \log n)$-approximation for the minimum linear arrangement problem, improving over the previous bound of $O(\log n)$.
@article {FL07,
AUTHOR = {Feige, Uriel and Lee, James R.},
TITLE = {An improved approximation ratio for the minimum linear
arrangement problem},
JOURNAL = {Inform. Process. Lett.},
FJOURNAL = {Information Processing Letters},
VOLUME = {101},
YEAR = {2007},
NUMBER = {1},
PAGES = {26--29},
}
This paper strengthens the main result of Euclidean distortion and the Sparsest Cut by showing that one can use a Fréchet embedding.
@article {ALN07,
AUTHOR = {Arora, Sanjeev and Lee, James R. and Naor, Assaf},
TITLE = {Fr\'echet embeddings of negative type metrics},
JOURNAL = {Discrete Comput. Geom.},
FJOURNAL = {Discrete \& Computational Geometry. An International Journal
of Mathematics and Computer Science},
VOLUME = {38},
YEAR = {2007},
NUMBER = {4},
PAGES = {726--739},
}
We prove that every \(n\)-point metric space of negative type (and, in particular, every \(n\)-point subset of \(L_1\)) embeds into a Euclidean space with distortion \(O(\sqrt{\log n} \log \log n)\), a result which is tight up to the iterated logarithm factor. As a consequence, we obtain the best known polynomial-time approximation algorithm for the Sparsest Cut problem with general demands. If the demand is supported on a set of size \(k\), we achieve an approximation ratio of \(O(\sqrt{\log k} \log \log k)\).
@article {LN08,
AUTHOR = {Arora, Sanjeev and Lee, James R. and Naor, Assaf},
TITLE = {Euclidean distortion and the sparsest cut},
JOURNAL = {J. Amer. Math. Soc.},
FJOURNAL = {Journal of the American Mathematical Society},
VOLUME = {21},
YEAR = {2008},
NUMBER = {1},
PAGES = {1--21},
}
We develop the algorithmic theory of vertex separators, and its relation to embeddings of certain metric spaces. As a consequence, we obtain an \(O(\sqrt{\log n})\)-approximation for min-ratio vertex cuts in general graphs based on a new SDP relaxation and a tight analysis of its integrality gap.
Our results allow yield algorithms for constructing approximately optimal tree decompositions of graphs. If a graph has treewidth \(k\), we find a tree decomposition of width at most \(O(k \sqrt{\log k})\). If, additionally, the input graph excludes a fixed graph as a minor, we produce a tree decomposition of width \(O(k)\).
Related: A similar method gives improved bounds for the minimum linear arrangement problem.
@article {FHL08,
AUTHOR = {Feige, Uriel and Hajiaghayi, Mohammadtaghi and Lee, James R.},
TITLE = {Improved approximation algorithms for minimum weight vertex
separators},
JOURNAL = {SIAM J. Comput.},
FJOURNAL = {SIAM Journal on Computing},
VOLUME = {38},
YEAR = {2008},
NUMBER = {2},
PAGES = {629--657},
}
[Note: This is the (unpublished) full version of a paper appearing in the SODA 2005 conference under the name Distance scales, embeddings, and efficient relaxations of the cut cone.]
We introduce a new number of new techniques for the construction of low-distortion embeddings of a finite metric space. These include a generic Gluing Lemma which avoids the overhead typically incurred from the naı̈ve concatenation of maps for different scales of a space. We also give a significantly improved and quantitatively optimal version of the main structural theorem of Arora, Rao, and Vazirani on separated sets in metrics of negative type. The latter result offers a simple hyperplane rounding algorithm for the computation of an \(O(\sqrt{\log n})\)-approximation to the Sparsest Cut problem with uniform demands, and has a number of other applications to embeddings and approximation algorithms.
For a more elegant and simpler proof of the “Big Core” Theorem, one can consult these notes of Rothvoss.
@inproceedings{DBLP:conf/soda/Lee05,
AUTHOR = {James R. Lee},
BOOKTITLE = {Proceedings of the Sixteenth Annual {ACM-SIAM} Symposium on Discrete
Algorithms, {SODA} 2005, Vancouver, British
Columbia, Canada, January 23-25, 2005},
PAGES = {92--101},
TITLE = {On distance scales, embeddings, and efficient relaxations of the cut
cone},
YEAR = {2005}
}
We present some new observations concerning the relation of finite subsets of $L_1$ to dimension reduction, topology, and Euclidean distortion.
@article {LMM05,
AUTHOR = {Lee, James R. and Mendel, Manor and Naor, Assaf},
TITLE = {Metric structures in {$L_1$}: dimension, snowflakes, and
average distortion},
JOURNAL = {European J. Combin.},
FJOURNAL = {European Journal of Combinatorics},
VOLUME = {26},
YEAR = {2005},
NUMBER = {8},
PAGES = {1180--1190},
}
We develop here a new multi-scale embedding method that we term measured descent and use it to resolve a number of open questions in the theory of embeddings of finite metric spaces.
@article {KLMN05,
AUTHOR = {Krauthgamer, R. and Lee, J. R. and Mendel, M. and Naor, A.},
TITLE = {Measured descent: a new embedding method for finite metrics},
JOURNAL = {Geom. Funct. Anal.},
FJOURNAL = {Geometric and Functional Analysis},
VOLUME = {15},
YEAR = {2005},
NUMBER = {4},
PAGES = {839--858},
}
Many classical problems in geometry and analysis involve the gluing together of local information to produce a coherent global picture. Inevitably, the difficulty of such a procedure lies at the local boundary, where overlapping views of the same locality must somehow be merged. It is therefore desirable that the boundaries be “smooth,” allowing a graceful transition from one viewpoint to the next. For instance, one may point to Whitney’s use of partitions of unity in studying what is now known as the Whitney extension problem.
In the present work, we consider what is perhaps the most basic Whitney-type extension problem, that of extending a Lipschitz function so that it remains Lipschitz. Often such a map is extended by first producing a cover of the new domain, extending the mapping locally, and then gluing together the individual pieces. Our main observation is that in many cases, if one chooses a random cover from the right distribution, the boundary can be made “smooth” on average, even when the local maps are individually quite coarse. This insight leads to the unification, generalization, and improvement of many known results, as well as to new results for many interesting spaces.
@article {LN05,
AUTHOR = {Lee, James R. and Naor, Assaf},
TITLE = {Extending {L}ipschitz functions via random metric partitions},
JOURNAL = {Invent. Math.},
FJOURNAL = {Inventiones Mathematicae},
VOLUME = {160},
YEAR = {2005},
NUMBER = {1},
PAGES = {59--95},
}
Announcement of Extending Lipschitz functions via random metric partitions.
@article{LNLip04,
AUTHOR = {Lee, James R. and Naor, Assaf},
FJOURNAL = {Comptes Rendus Math\'ematique. Acad\'emie des Sciences. Paris},
JOURNAL = {C. R. Math. Acad. Sci. Paris},
NUMBER = {11},
PAGES = {859--862},
TITLE = {Absolute {L}ipschitz extendability},
VOLUME = {338},
YEAR = {2004}
}
We show that every embedding of the level $k$ diamond graph of Newman and Rabinovich into $L_p$ with $1 < p \leq 2$ requires distortion at least $\sqrt{k(p-1)+1}$. An immediate corollary is that there exist arbitrary large $n$-point subsets $X \subseteq L_1$ such that any $D$-embedding of $X$ into $\ell_1^d$ requires $d \geq n^{\Omega(1/D^2)}$. This gives a simple proof of the $L_1$ dimension reduction lower bound of Brinkman and Charikar.
@article {LNdiamond04,
AUTHOR = {Lee, J. R. and Naor, A.},
TITLE = {Embedding the diamond graph in {$L_p$} and dimension reduction
in {$L_1$}},
JOURNAL = {Geom. Funct. Anal.},
FJOURNAL = {Geometric and Functional Analysis},
VOLUME = {14},
YEAR = {2004},
NUMBER = {4},
PAGES = {745--747},
}
We study the quantitative ditsortion required to embed finite, uniformly doubling metric spaces into normed spaces.
@inproceedings {GKL03,
author = {Anupam Gupta and
Robert Krauthgamer and
James R. Lee},
title = {Bounded Geometries, Fractals, and Low-Distortion Embeddings},
booktitle = {44th Symposium on Foundations of Computer Science {(FOCS} 2003), 11-14
October 2003, Cambridge, MA, USA, Proceedings},
pages = {534--543},
year = {2003},
doi = {10.1109/SFCS.2003.1238226},
}
We resolve a conjecture of Levin together with Linial, London, and Rabinovich about embeddings of graphs whose intrinsic metric has polynomial growth. We also resolve positively a related embedding question of Benjamini and Schramm.
@article {KL07,
AUTHOR = {Krauthgamer, Robert and Lee, James R.},
TITLE = {The intrinsic dimensionality of graphs},
JOURNAL = {Combinatorica},
FJOURNAL = {Combinatorica. An International Journal on Combinatorics and
the Theory of Computing},
VOLUME = {27},
YEAR = {2007},
NUMBER = {5},
PAGES = {551--585},
}